Generalizing Digital Waveguides for Composition
Abstract
We present a number of extensions to digital waveguide synthesis, each adapted to a specific compositional application. Variations discussed include unconventional excitation functions, variations on waveguide section structures and network configurations, peak-limiting strategies for unconventional gain structures, and multichannel spatialization techniques. The compositional motivations for these techniques range from the “surreal” extension of musical instrument models, to more abstract soundscapes possessed of the articulate and musical features of physical modeling synthesis.
Introduction
One-dimensional digital waveguides are widely used in the computer music community to model acoustic waves propagating along different media, such as strings and tubes. The waveguide approach enables the simulation of different musical instruments, including plucked, struck, and bowed strings, woodwinds, and percussion. Digital waveguides are efficient (with a low cost realtime implementation) and provide a meaningful physical interpretation.
The idea behind digital waveguides was first introduced by McIntyre, Schumacher, and Woodhouse in the early 1980s (McIntyre, Schumacher and Woodhouse 1983). They discovered that different classes of musical instruments, such as a bowed string, a flute and a clarinet, could all be modeled with a nonlinear excitation coupled to a linear resonator. Julius Smith developed this idea further and introduced digital waveguide theory (Smith 1992). More recently, Georg Essl has proposed extensions to and abstractions of waveguide models which facilitate the simulation of non-physical (or “surreal”) behavior (Essl 2003).
In this paper we propose a “generalized” digital waveguide, which facilitates both the creation of extended physical models, and the application of waveguide synthesis in situations without a physical interpretation. The generalized waveguide can encompass a variety of excitations, delay configurations, network topologies, gain structures, and spatialization techniques. The following sections describe these specific waveguide extensions, as well as the compositional applications which spurred their development.
Excitations: nonlinear functions, soundfiles, and live inputs
Our first experiments with unconventional excitations involved unusual nonlinear excitation functions, such as a velocity dependent friction curve to simulate rubbing different hard surfaces, and a pressure dependent nonlinear function to reproduce blowing on different surfaces. In both cases, the waveguide resonator was coupled to the sustained nonlinear excitation in a feedback loop.
Beyond excitation via mathematical functions, both soundfiles and live audio inputs can be used to drive waveguide networks. For example, we used sampled excitation functions to model rich impulsive excitations such as struck plates and bowls. The excitation was obtained by recording different objects struck at different positions, and then removing the main frequency components using spectral analysis and inverse filtering. The filtered result was fed into the waveguide resonator in a feed-forward loop.
The use of soundfiles as excitations relates to the use of waveguide networks to simulate reverberation; however, more esoteric transformations are also possible. For instance, it is possible to compose continuous transitions between soundfile reverberation and feedback generation, through careful control of delay lengths and gain coefficients.
We have also designed networks which are excited by live audio inputs. Depending upon the network topology and system gain, microphones don’t even have to be plugged in to excite the network; self-noise at the analog-to-digital converter may be sufficient to set the process in motion. These setups, as in the John Cage realization described below, can produce complex and interesting interactions between the activities of a live performer and the output of the network.
Gain structure: peak-limiting strategies
Traditional waveguide topologies, like other signal processing elements which involve feedback (e.g., IIR filters) are explicitly designed to preserve system stability. However, it is possible to impose bounded amplitudes in signal processing systems which do not meet traditional criteria for stability. For instance, local peak control can be implemented via waveshaping with “soft clipping” nonlinear functions. Charles Sullivan presented one such function in his work on physical models of the electric guitar (Sullivan 1990):
2/3; x >= 1
f(x) = x - x3/3; -1 < x < 1
-2/3; x <= -1
Related methods for amplitude management include peak-limiting compression and the “elastic-mirrors” in Xenakis’ GENDYN technique (Xenakis 1992, Hoffmann 2000).
Nonlinear waveshaping functions necessarily color the sonic output of a system, especially when nonlinearities are deployed at several different points in a network. While this timbral alteration may seem like a disadvantage, in a compositional context it can just as well be viewed as a desirable feature. After all, peak-managed feedback networks are of interest precisely because they encourage non-physical designs with unusual sonic characteristics.
Waveguide section and network structure: unconventional configurations
Peak-management techniques allow a rethinking of the elements and connections within a single waveguide. Many of the waveguides tested in our work feature continuously changing delay lengths, including dynamic delay lengths independent for each rail of a waveguide. Some sections tested even forego the notion of rails, placing delays in configurations which cannot be interpreted physically.
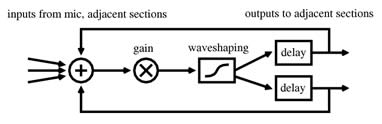
Similarly outside of the domain of physical interpretation, peak management makes it possible to eliminate the typical inversion of polarity as a signal passes between rails of the waveguide (Smith 1987). Waveguides which don’t utilize sign changes tend to output DC. However, they can be encouraged to produce audible signals if they are perturbed, through changes to the gain coefficients, the delay lengths, or the excitation.
As waveguide sections are combined into larger structures, nonlinearities and other forms of peak management facilitate a wide range of network topologies, eliminating concerns about the gain structure of a particular architecture (Essl and Cook 2002). Our experiments have focused on circular architectures (networks without a particular beginning or end), including structures with “spokes” connecting nonadjacent sections.
Spatialization
A natural extension of the physically-based waveguide network is the independent spatialization of individual waveguides. By distributing the waveguides of a physically-based system around the listener, the notion of “body” as perceived from an exterior orientation, and the perceptually interior notion of “space,” can be modulated. Spatial modulation of the system allows for an extended notion of the objecthood of the model, and the possibility of transforming it from body into space, or from object into environment. In previous work, the authors have explored extended techniques for physical models by taking advantage of the disassociation of the synthesis and control aspects of the virtual instruments (Serafin, Burtner, Nichols, and O’Modhrain 2001, Burtner and Serafin 2001).
Building on this work, the physical model of the Tibetan singing bowl suggested an extended approach to spatialization for waveguide networks. A bowl model was implemented allowing each of eight waveguides (each representing a different mode of the bowl) to be controlled independently. In order to explore the acoustic effect of moving from an exterior to an interior position of the bowl, the impulse response of the bowl was taken from different locations in and around the bowl. Microphones placed inside the center of the bowl, 30cm above the bowl, and 20cm to the side recorded the different impulse responses of the bowl. From these recorded impulse responses, we extracted the frequencies of the main resonances of the instrument, together with the corresponding damping factors, using spectral analysis. The modeling of the multichannel bowl has been discussed in greater depth elsewhere (Burtner and Serafin 2002).
The resulting instrument, implemented as an extension to the Max/MSP environment, allows simultaneous independent control of the eight modal frequencies, eight decay times for the low-pass filters, eight bandwidths for the resonant filters, four dispersion coefficients for the allpass filters, one input for an external source of energy, one excitation position (i.e. where the bowl is hit), one excitation pressure (i.e. how hard it is hit) and one excitation velocity. Eight outlets, each outlet corresponding to a mode of the resonant structure, are sent to spatial processing algorithms for diffusion through a multichannel loudspeaker configuration.
The spatial transformations of the physically-based waveguide networks represent a desire to explore extensions of physical modeling synthesis. The possibilities for the embodiment of the model are broadened. The virtual body is not confined to the same limitations as the physical body, and an extended technique is explored that blurs the boundaries between resonating body and acoustic space. Multi-channel diffusion of the modes stresses the coherence of the model, pulling apart the synthesis into constituent percepts as the components are treated separately in space. This technique has been identified as an example of Spatio-Operational Spectral (SOS) Synthesis, and discussed in greater detail elsewhere (Topper, Burtner, and Serafin 2002).
For waveguide networks composed of discrete sections arranged in a circular topology, a direct approach to spatialization is to output each section “in position". For example, eight discrete sections of the type presented in Figure 1 can be arranged in a circle, with the output of each section routed to its own loudspeaker. If the loudspeakers are arranged in a matching circular configuration, the result is a sonification of the propagation of energy through the network. In this situation it becomes possible to hear the influence of particular regions of the network on their adjacencies. While there is no panning or simulation of motion in the conventional sense, cascades of audible activity around the network can produce a variety of compelling spatialization effects.
Musical applications: generalized waveguides in practice
1. That which is bodiless is reflected in bodies
In Matthew Burtner’s musical composition That which is bodiless is reflected in bodies, SOS synthesis is used to explore the threshold between physical and non-physical reality. The composition takes as its starting and ending point the physical model bowl as a true acoustic representation of the physical body. In the piece, the physical object is transformed and explored as a multidimensional space that gradually disintegrates into non-physical reality. The compositional process in the pieces draws on a gradual disembodiment and reimbodiment of the acoustic nature of the bowl’s physicality. In order for the physical model to become a transformative immersive environment, the possibility of recreating a spatial representation of the transformational modal bowl is explored in the composition. Changes in modal properties of the bowl effectively alter the size and shape of the bowl. If the physical model bowl were a real bowl, it would be seen changing dynamically in space. Extending this principle from an exteriorization of sound to an interior perspective, if the listener is positioned inside the bowl as a type of room, the room would be changing shapes around the listener.
In order for the listener to effectively experience these changes in a performance context, modal transformations of the bowl are linked with spatial propagation of the sound. To accomplish this, each mode of the multichannel bowl discussed above, was assigned to a separate, distinct audio channel. Figure 2 details the implementation of this configuration.
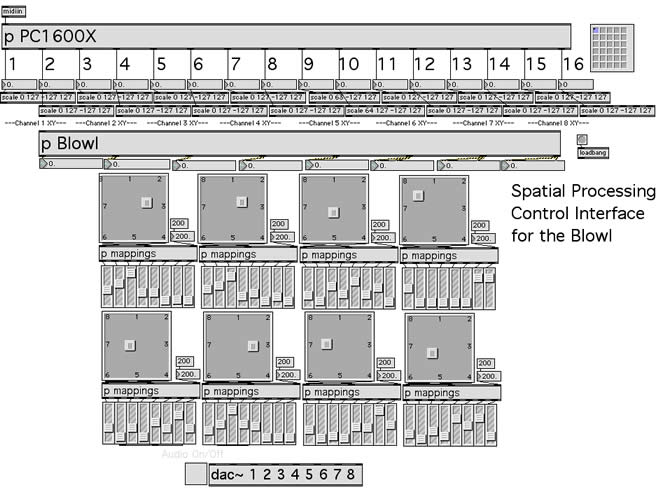
The output of the modes are coordinated in a spatial configuration surrounding the listener. As the modes change, the spatial location of the signal changes accordingly. That which is bodiless is reflected in bodies draws the listener close to and then inside the acoustics of the resonating bowl. Once inside the bowl, the modes are multiplied generationally, and the sound environment diverges from any physical representation, becoming an abstract auditory environment built from waveguide networks. That which is bodiless is reflected in bodies offers an initial example of how physically-based modal waveguide synthesis can function as an extended technique in combination with spatial processing.
2. Electronic Music for Piano
Our first application of a peak-managed feedback network was for a realization of John Cage’s Electronic Music for Piano (Cage 1965). In keeping with the increasingly improvisatory nature of Cage’s approach to music with live electronics during the 1960s, the handwritten prose score of Electronic Music for Piano is suggestive, not prescriptive. Inspired by and in appreciation of Cage and especially dedicatee David Tudor’s work in the domain of feedback, Christopher Burns designed this version around a feedback network, implemented using Miller Puckette’s Pd software (Puckette 1996). The feedback network is the most prominent of several parallel signal processing chains applied improvisationally to a live performance of Cage’s Music for Piano 69-84 (Cage 1956). The network represents the most extreme form of signal processing in the realization, in that the sustaining, swooping output sounds utterly unlike the piano input.
The feedback section of the instrument passes the two microphone inputs into a circular chain of delay structures, with sixteen delay lines grouped in eight sections. Although each section has two delays, these are not configured as upper and lower rails - the polarity inversion between rails can be engaged or bypassed independently for each rail by the operator, and each of the delay lines has a continuously variable length. These lengths are randomly and independently generated for each delay, as are the sweep and sustain times which control the transitions between each new length.
Despite the emphasis on the algorithmic generation of low-level parameters, there is a role for an electronics operator to improvise and intervene during the performance. The operator has access to global scaling factors for each of three delay parameters (delay length, sweep time, sustain time). These scaling factors allow the operator to compress or expand the parameter ranges available to the algorithms. There is also a single parameter controlling all the (identical) gain coefficients of the network. This is certainly the operator’s single most influential parameter over the behavior of the network. As mentioned above, the operator can perturb the network by selectively engaging or bypassing the polarity inversion in each generalized waveguide section. Finally, the operator has eight selectable output volume presets, each of which independently modifies the output gain stages associated with the eight different loudspeakers, as well as the ability to mute individual loudspeakers. Each preset has its own spatial distribution and weighting of different segments of the feedback network.
The electronics operator, through the parameters mentioned above, and the pianist, via the microphone inputs, can influence the feedback network. However, they do not command it. The network performs in unpredictable ways, sometimes imitating onsets and pitches played at the piano very precisely, sometimes remaining quiet during busy passages, sometimes bursting into noise in the middle of a long silence. Because the polarity inversion is typically not present in every section, the network tends towards the inaudible output of DC. The pianist can perturb the system into audibility by providing an excitation; the electronics operator can encourage the system to sound by raising the gain coefficients near unity, by applying and removing polarity inversions, or by seeking a new configuration of delay lengths. The operator can also reliably squelch the feedback network output by turning the gain coefficients down to zero, or by muting the loudspeakers.
The unpredictable behavior of the destabilized feedback network, enhanced by the algorithmic generation of many of its parameters, is the primary feature of the Electronic Music for Piano realization. There is a symbiosis of piano, pianist, electronics, and operator; in performance the situation is one of improvising with the electronics, rather than using the electronics to improvise. The electronics are designed to guide the operator’s musical choices just as the operator guides the electronics. The emergent aspects of the realization’s behavior help foster intense listening and communication between pianist and electronics operator in performance.
3. Hero and Leander
Following the Cage realization, more recent applied work with generalized waveguide networks utilizing peak management has focussed on the composition of multichannel tape music. In the more fixed environment of tape composition, the indeterminate aspects of the Cage realization’s feedback network are less desirable, and so for the composition of Christopher Burns’ Hero and Leander we have implemented a new and more pliable version of the network in Bill Schottstaedt’s Common Lisp Music environment (Schottstaedt 1994).
Like the Cage realization, the new design is built from a circular arrangement of eight sections. However, each section is much more closely modelled on a traditional waveguide, and therefore more stable and less likely to output DC, than in the Cage realization. The designs include upper and lower rails, and four of the eight sections include a polarity inversion. (If all eight sections included the sign change, the results would be more like a conventional physical model, and less like the characteristic feedback sound of the Cage realization).
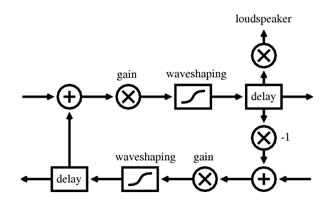
Figure 3 demonstrates the structure of one the sections which includes the polarity change. Compared to the operator’s control over the Cage realization, the control parameters for this network are numerous and low-level. The excitation function is an arbitrary multichannel soundfile. The instrument provides time-varying envelopes for each of the sixteen delay lengths, plus one time-varying envelope which controls all the gain coefficients. If complex envelopes are used, there can be a large amount of information to specify. However, this parameterization provides for a wide variety of results, with a substantial amount of control over the sonic details of the network’s output. Articulation characteristics and other sonic details are not exposed directly to the composer as parameters, but are accessible through the influence of delay lengths and gain coefficients.
Conclusions: Waveguides beyond physical modeling
The flexibility of waveguide synthesis allows composers to create different virtual instruments that are interesting from a musical perspective. Among the most interesting compositional applications of waveguides are those that seek to transcend the limitations of the acoustic models which govern their configuration. A generalizing perspective on waveguide synthesis facilitates the creation of both “surreal” and abstract sonic textures beyond the possibilities of strictly physical simulations.
References
Burtner, Matthew and Stefania Serafin. ‘Extended Techniques for Physical Models using Instrumental Controller Substitution’, in Proceedings of the International Computer Music Conference 2001. La Havana, Cuba, 2001.
_____. ‘Strictly Bowlroom: the physically modeled singing bowl in a transformative immersive environment’, in Proceedings of ISMA, Mexico-City, Mexico, 2002.
Cage, John. Music for Piano 69-84, Henmar Press 1956.
_____. Electronic Music for Piano, Henmar Press, 1965.
Essl, Georg. ‘The displaced bow and APhISMs: abstract physically informed synthesis methods for composition and interactive performance’, in Proceedings of the Florida Electroacoustic Music Festival 2003.
Essl, Georg and Perry Cook. ‘Banded Waveguides on Circular Topologies and of Beating Modes: Tibetan singing bowls and glass harmonicas’, in Proceedings of the International Computer Music Conference, ICMA, 2002, pp. 49–52.
Hoffmann, Peter. ‘The new GENDYN program’, in Computer Music Journal, vol. 24, no. 2, pp. 31–38, 2000.
McIntyre, M., R. Schumacher, and J. Woodhouse. ‘On the oscillations of musical instruments’, in Journal of the Acoustical Society of America, vol. 74, no. 5, pp. 1325–1345, Nov. 1983.
Puckette, Miller. ‘Pure data’, in Proceedings of the International Computer Music Conference, ICMA, 1996, pp. 269–272.
Schottstaedt, Bill. ‘CLM — Music V meets Common Lisp’, in Computer Music Journal, vol. 18, no. 2, pp. 30–37, 1994.
Serafin, Stefania, Matthew Burtner, Charles Nichols, and Sile O’Modhrain. ‘Expressive controllers for bowed string physical models’, in Proceedings of DAFX 2001, Limerick, Ireland, 2001.
Smith, Julius O. ‘Waveguide Filter Tutorial’, in Proceedings of the International Computer Music Conference, ICMA 1987, pp. 9–16.
_____. ‘Physical Modeling using Digital Waveguides’, in Computer Music Journal vol. 16, no. 4, pp. 74–91, Winter 1992.
Sullivan, Charles. ‘Extending the Karplus-Strong Algorithm to Synthesize Electric Guitar Timbres with Distortion and Feedback,’ Computer Music Journal, vol. 14, no. 3, pp. 26–37, 1990.
Topper, David, Matthew Burtner, and Stefania Serafin. ‘Spatio-Operational Spectral (SOS) Synthesis’, in Proceedings of Cost-DAFX, Hamburg, Germany, 2002.
Xenakis, Iannis. Formalized Music. New York: Pendagron Press, 1992.
Social top