Conditioning Compositional Choice

Theoretical imperatives and a selection algorithm using converging value sets

by Sean Peuquet

I recall Mark Applebaum once saying that most of his creative work stems from asking himself the question, “What would happen if…?” 1[1. In the context of a composition masterclass that Applebaum led while in residence at the University of Florida in February 2011.] His explanation struck me immediately, and intuitively I felt it to be true, as it so perfectly reflected how I too begin to consider and ultimately generate enthusiasm around new compositional behaviour in my own artistic activities. Applebaum’s question is focused on action and, fundamentally, the hope one retains for the activity of composition and its effects, its potential outcomes; what follows the “if…” is undoubtedly a construction of a subject and an action verb. Accordingly, I’ve come to think that the question prioritizes “boots on the ground” composition, whereby “compose” — notably absent from Applebaum’s first line of creative thought — is a verb, first and foremost, an action that must be performed in a particular place and time, the imperative of which we weaken when we turn it into a noun. Which leads me to wonder what actions one might take in a particular place and time? What, as a matter of concrete activity, follows the “if…”? And already we are back in the domain of thinking instead of doing. But it is my contention that thinking about composition (as a process, as a noun) can help us to reframe the second-order question of what can, and perhaps should, follow the “if…” as a matter of engaged action.

So at the risk of perpetuating a perhaps quaint and unnecessary distinction between doing and thinking, and (at least for the purposes of the present discussion) prioritizing the latter, 2[2. I in no way intend to insinuate Applebaum’s work lacks thought. Merely, I am curious about what happens (what questions might we ask) when we allow analysis of process to take priority over pure enactment.] I ask, “On what ground does composition take place?” Across the remainder of this text, I formulate one possible set of conditions in response to this question, and propose one very general technique as a response to such conditions.

Taking Place

Over the past few years, I have shifted my practice away from the composition of works for concert performance and toward the construction of objects and experiences loosely categorized under the umbrella terms “installation” and “sound art”. This shift emerged as a response to my interrogation of place — of music necessarily taking place through the activity of composition, performance and listening. The idiom “to take place” refers to an occurrence, an act of spatio-temporal significance or consequence. But more literally, “to take” is to possess, and further, to possess by way of subtraction (“to take from”). Music taking place thus suggests an occurrence of possession; she who composes, performs or listens takes from (and assumes as her own) the literal and discursive territory she inhabits. I am here reminded of how Yi-Fu Tuan made a passing comment on Roberto Gerhard’s statement about musical form: “Form in music means knowing at every moment exactly where one is. Conscious form is really a sense of orientation” (Tuan 1977, 15). The notion of taking possession, the place in which such taking occurs, and the place that is also constituted through such taking carries three implications. First, that under the conditions of finitude — of always-already being placed here and not there, where here is given to us bodily and sensorially and there is not — we must take one thing and not another. Or, perhaps more simply: to take is always to take from that which remains. 3[3. Even to say, “Take the Universe…,” concedes that the universe is not all there is to take. In fact, at the precise edge of our astrophysical understanding of our place in the universe, our place is perhaps one of multiple (infinite?) self-similar places (observable universes) if we are to take the multiverse into consideration. And it is precisely the scope of inclusion regarding what we mean when we refer to multiverse that remains in question — a fuzzy limit, against which we weigh both the objective and subjective conditions for nothingness, the place of no-place at all. This limit, its very fuzziness, is where ontology appears incomplete and, in complimentary fashion, epistemology appears uncertain.] Second, in consideration of this remainder, to take reflects a choice over that which is taken and that which is not. And third, that choice (to take from here and not there) prioritizes and elevates something specific over its generic remainder.

Choice and Limitation

These observations are hardly new. I am merely echoing Herbert Brün’s old but increasingly relevant assertion that “Where there is no choice there is no Art” (Brün 2004, 3). Choice, following Brün, is a necessary condition for art to be anywhere (insofar as being-at-all entails being-there, cf. Heidegger’s Dasein). In recognition of where we are (physically, cognitively, perceptually), we artists identify a need to choose and, as a result of our choices, there is art. The situation we find ourselves in is needing to make a choice regarding what there is to be in the place where we always-already are; we are where we are when we need to make a choice of artistic consequence. Therefore, we acknowledge that we are part of the place from which we seek to take. However, taking ourselves (our limitations and their inherent remainder) in the place we are is not a sufficient choice for there to be art. Brün immediately limits such possibility when he says:

The personality of a person is neither that person’s nor anybody’s choice, therefore it can not be considered as relevant to Art nor useful as an instrument of an Artist. It is good choosing that makes the Artist a personality, not the personality that makes a good chooser. (Brün 2004, 3)

Brün not only excludes personality as a consideration relevant to the content of art, but further excludes the usefulness of personality as artistic instrument. Such exclusion also implies that, given the necessity to make choices, the artist must also confront her choice over what instrument she will use to enact or realize further choices. Here, we should embrace the broadest possible interpretation of “instrument”, from Charlie Chaplin’s cane to Cage’s I-Ching.

Place and Repetition

Articulating a more general difference between mere being-there and taking place, French philosopher Alain Badiou (with recourse to Mallarmé) effectively recapitulates Brün’s exclusion of the self (vis-à-vis personality) as a true choice. He does so by excluding the possibility for any truth to proceed on the grounds that nothing takes place:

In order for the process of a truth to begin, something must happen. As Mallarmé would put it, it is necessary that we be not in a predicament where nothing takes place but the place. For the place as such (or structure) gives us only repetition, along with the knowledge which is known or unknown within it, a knowledge that always remains in the finitude of its being. (Badiou 2004, 111)

Knowledge, of course, presupposes the subject who knows. Thus, “where nothing takes place but the place,” we find ourselves subject to nothing other than our own perceptual limitations and (lack of) knowledge. That old Zen truism, “Everywhere you go, there you are,” 4[4. That this saying appears as the title of a Jon Kablat-Zinn’s “mindfulness” book from 2004 (see Kablat-Zinn 2004), also serves to nicely connect Badiou’s “place as such (or structure) [giving] us only repetition” with the burgeoning marketplace for Zen-inspired self-help. Which is to say that in such a place (the place of Late Capitalist enclosure), form and content overlap and provide no critical outside, no there there.] nicely illustrates this very same predicament described by Badiou, that place of pure repetition. The truth of any choice, or identification of a choice to be made, arises in response to some change of circumstances (alleviation of the predicament of being-there, again and again). A true choice, therefore, cannot simply be the consequence of being ourselves where we are, but rather must proceed in light of some difference — to ourselves where we were (or will be), or to the place where it was (or will be) — either real or imagined. Which is to say, the necessity that “something must happen” is an unavoidably temporal phenomenon, a change that reconstitutes the place as given, as well as our part in it. If Brün’s exclusion of personality from the category of things that may be chosen reveals the instrumental and hierarchical nature of choice, then Badiou’s exclusion of the place in which nothing happens from the category of places that may give rise to truths (and thus true choices) reveals the temporality of choice, of choice as both a response to change and an agent of change.

Non-Triviality

Thus, to consider the place in which something happens is to consider those changes that implicate one’s comportment vis-à-vis the world. Things change around us all the time, affecting our behaviour under the guise of our passive acquiescence to, or active reconfiguration of, concrete limitations. Michel de Certeau frames these modes of behaviour nicely, when he describes the everydayness of walking in the city as both the actualization and invention of possibility:

First, if it is true that a spatial order organizes an ensemble of possibilities (e.g., by a place in which one can move) and interdictions (e.g., by a wall that prevents one from going further), then the walker actualizes some of these possibilities. In that way, he makes them exist as well as emerge. But he also moves them about and he invents others, since the crossing, drifting away, or improvisation of walking privilege, transform or abandon spatial elements. Thus Charlie Chaplin multiplies the possibilities of his cane: he does other things with the same thing and he goes beyond the limits that the determinants of the object set on its utilization. In the same way, the walker transforms each spatial signifier into something else. And if, on the one hand, he actualizes only a few of the possibilities fixed by the constructed order (he goes only here and not there), on the other he increases the number of possibilities (for example, by creating shortcuts and detours) and prohibitions (for example, he forbids himself to take paths generally considered accessible or even obligatory). He thus makes a selection. (de Certeau 1984, 98)

We should reinforce here that the selection any city walker (or for that matter composer) makes is always double. Any selection made vis-à-vis the world carries with it a selection vis-à-vis the self — to actualize interdictions given a passive stance or to invent possibilities given an active one. However, the selection regarding one’s subjective stance is only realized through the more immediate, engaged selection of what to do given the “constructed order”. Thus there is no reason to directly choose oneself; he who chooses is retroactively chosen through the very process of making a choice in the world. Which, in more philosophical terms, is (according to Žižek) a deeply Hegelian notion, regarding the Spirit of one’s concrete engagement in the world, that runs counter to the standard textbook reading of Hegel:

When Hegel says that a Notion is the result of itself, that it provides its own actualization, this claim which at first cannot but appear extravagant (the notion is not simply a thought activated by the thinking subject, that it possesses a magic property of self-movement…), loses its mystery the moment we grant that the Spirit as the spiritual substance is a substance, an In-itself, which sustains itself only through the incessant activity of the subjects engaged to it. Say, a nation exists only insofar as its members take themselves to be members of this nation and act accordingly; it has absolutely no content, no substantial consistence, outside this activity. (Žižek 2012, 187)

Accordingly, he who walks the city, actualizing a few fixed possibilities and inventing new ones, makes a selection regarding the Spirit of his commitment, his engaged activity, only as a product of that activity; “the Self to which spirit returns is produced in the very movement of this return” (Žižek 2012, 186). The temptation to choose oneself outright, as an a priori (Artist) personality endowed with an ability to make good choices, thus reflects a desire to turn away from the choice of consequence, the true choice: to actualize fixed possibilities or to invent new ones.

It is not unreasonable, then, to consider, in further reinforcement of de Certeau’s larger point regarding consumption and production, that consumption of what is readily available can itself be productive — can serve to actualize or to invent. This is a proper way to consider making compositional choices, as a matter of actualization or invention given the territory in which one already finds oneself, or the territory one has already chosen. Thus, to make a productive choice, one that serves to constitute a new territory of affordance or possibility, is to act (even through one’s passivity) in what Brün would call a “non-trivial” way. The non-trivial person, “is an output to society but, in being this output, changes it to such an extent in himself that when he now feeds it back, it turns into an input” (Brün 2004, 78).

Circumscribing Functional Obligations

What we have established so far is that for art (and thus composition) to take place, one must make choices; that each choice must have a remainder; that a true choice requires something to happen; that what happens must not simply be where it happens (the place alone) nor the person’s personality in the place they always-already are; that what happens when one identifies or makes a true choice happens in time; and that any choice regarding how one identifies or makes a true choice is similarly true (that is, subject to the above conditions) or not. Which is to say, choice is reflexive. This last point, regarding the reflexivity of choice, is where choice becomes non-trivial (in the cybernetic, Brünian sense of the word) and, by extension, further implicates the chooser in carrying the burden of choice — of needing to make good choices to make herself, the Artist, a personality.

Such a circumscription of the functional obligations that condition any compositional choice applies as much to The Eroica as it does to Variations for Orchestra, or even Cage’s 0’00” 5[5. I would argue that 0’00” reflects a true compositional choice in the following way: Cage chose to defer to the performer to choose how to “perform a disciplined action.” The adjective “disciplined” is Cage’s critical choice here. For without it, he ran the risk of allowing the possibility that any performer could self-select their own personality and qualify whatever action such a personality might have produced in the moment as being the piece. Discipline, however, requires control — control over oneself so as to not present merely oneself. Therefore, something happens: one is held in opposition to (as different from) oneself. And thus we avoid the predicament where nothing takes place but the place.] — which is not to say that such considerations are general to the point of being meaningless, but rather are necessarily inclusive of various compositional practices that at one time or another served to stretch the bounds of music composition. While any number of performance art pieces could be read as a staging of Cage’s 0’00” (not least of which is Marina Abramović’s 2010 piece, The Artist is Present), we can both imagine and identify propositional art that fails to reflect any true compositional choice in light of the above conditions. For example, Marni Kotak’s Birth of Baby X reflects nothing other than a mother in the place she is when her baby is born, or, conversely, a baby insisting upon its own being-there. Or, as another example, recall actor James Franco’s turn as the artist “Franco” on the soap opera General Hospital in 2009; read: a performing actor’s choice to become a performance artist by choosing himself to act the role.

Failure to reflect true compositional choices that ultimately actualize or invent possibilities given an (often hierarchical) territory of compositional limitation and affordance is perceived as a failure of the resultant art. A composer’s responsibility over all the choices made in a piece of music (to ensure it doesn’t fail) can surely be daunting, but is only “complete” as a matter of discursive attribution, never as a matter of material practice. Imprecision, idiosyncrasy and contingency find a way in.

Choice of Method

Responsibility and Accountability

We composers implicate ourselves in a call to action given our identification of needing to choose. Identification of choice insists upon the identification of oneself as a potential actor responsible for either choosing to act (by making a choice) or choosing not to. There is art only insofar as one assumes not only such responsibility but also, more importantly, the capacity to choose and a basis for choosing as a matter of functional obligation and moral reasoning, respectively. If we accept that a composer’s responsibility to make choices is never absolute, that choice is always (on some level) deferred, contingent or simply incomplete, then we can begin to evaluate one’s capacity to choose (functional obligation) not as a matter of proportion (read: rigour), but rather as a matter of scope or chosen level of abstraction. This means that a basis for choosing is always-already of critical concern given the composer’s need to choose the level at which they will choose (specify) musical materials. The moral obligation to consider a basis for choosing enters at the ground floor.

Given both functional and moral obligations that condition responsible artistic action, we face the question of accountability. If, as activist Geoff Hunt writes, accountability “is the readiness or preparedness to give an explanation or justification to relevant others (stakeholders) for one’s judgments, intentions, acts and omissions when appropriately called upon to do so” (Hunt cited in Bivins 2006, 21), then we ask, to whom is the artist accountable and when will they be called upon to account? Or, what is at stake in making a compositional choice and who holds its shares? The classical answer is some abstract notion of “audience” given the assumption the piece is ever performed (which is akin to saying the “market” today); the New Age answer is the composer herself via her own self-relating and personal “growth”; and the more speculative answer I subscribe to is probably nobody in a future that is, nevertheless, contingent (at least in part) upon the composer making the choice anyway.

Given the absence of “stakeholders”, can we nevertheless consider a “better” or “worse” basis for choosing? If levels of abstraction are inherently at play when we consider how one should choose how to make musical choices, then the previous discussion of de Certeau’s example of walking the city should give us a clue.

Making the “Wrong” Choice

We have identified true choices as those that actualize fixed possibilities or invent new ones. Yet, in recognition of what de Certeau describes as those “possibilities fixed by the constructed order,” the difference between actualization and invention vis-à-vis possibility is a more fundamental choice. Ultimately, this choice concerns one’s reinforcement of the constructed order, or ability to instigate a more “violent” rupture that breaks protocol. Here, Žižek, again articulating a non-standard Hegelian perspective on the French Revolution, provides some insight:

Only the “abstract” Terror of the French Revolution creates the conditions for post revolutionary “concrete freedom.”

If one wants to put it in terms of choice, then Hegel here follows a paradoxical axiom which concerns logical temporality: the first choice has to be the wrong choice. Only the wrong choice creates the conditions for the right choice. Therein resides the temporality of a dialectical process: there is a choice, but in two stages. The first choice is between the “good old” organic order and the violent rupture with that order — and here, one should take the risk of opting for “the worse.” This first choice clears the way for the new beginning and creates the condition for its own overcoming, for only after the radical negativity, the “terror,” of abstract universality has done its work can one choose between this abstract universality and concrete universality. (Žižek 2012, 289–290)

There is risk to using the city in unconventional ways — risks that any skateboarder or parkour traceur would be all too keenly aware of. And, similarly, there are risks to composing as an outright rejection of historical precedent and pre-given technologies; though, such risks are mostly socio-cultural and economic, and not physical. The radical nature of our investigation, nevertheless, becomes clear: one should choose to invent possibility itself, even if it appears the “worse” choice given the immediate conditions. For only through a radical departure can we carve open the space for new concrete practices to emerge.

Method as Limitation

We can, in light of the imperative to invent possibility itself, clearly discern the contours of both Schoenberg’s twelve-tone system and Cage’s deployment of chance procedures as having each fulfilled a moral obligation to make the “wrong” choice.

Despite Cage’s disavowal (in the late forties) of his tetrad of Structure, Method, Material and Form as domains of compositional choice (Cage and Charles 1981, 39), it is hard not to see his choice of applied chance procedures as a commitment to, if not outright prioritization of Method. When all is stripped bare, and environmental sounds become heard as music, does not the framing of sound and the method by which the frame became specified remain? If compositional method lingers in the absence of other domains of choice, then we should, following Cage, prioritize and readdress it.

Accepting the social, economic and psychological significance of what Barry Schwartz has famously called the paradox of choice (Schwartz 2004) — the principle that there are too many consumer choices, which, in effect, outstrips our cognitive capacity to make a qualified choice — to choose a method of choosing is perhaps most important today, purely to help limit the options. Furthermore, if the unbridled proliferation of choice is a direct consequence of mass production and extensive automation, then at the outset we must decide to follow the formalized modes of production the modernist break heralded, or instead be lured into postmodernism’s reactive formations of frames devoid of content, whereby any “transgressive excess loses its shock value and is fully integrated into the established art market” (Žižek 2012, 256). Under such postmodernist conditions, radical art is just another domain of consumer choice. Accordingly, our fidelity to formalized, rule-based methods of composition now appears to be the “wrong” yet necessary choice to make.

Given the philosophical considerations we have so far entertained as a means to situate the activity of composition vis-à-vis decision-making (following both functional and moral obligations), we now seek an applied practice. Given the priorities outlined above, we should target our efforts toward the development of a compositional Method. In full agreement with Stephen Wolfram’s recent observation that “it’s really an interesting time, because it’s a time when philosophy gets implemented as software, basically” (Reese 2015), the remainder of this text focuses on making choices regarding the development of a mechanistic tool for making choices.

A General Computational Technique

As a selection algorithm, James Tenney’s implementation of a statistical feedback model points us in the right direction. As Larry Polansky, Alex Barnett and Michael Winter describe, Tenney’s “dissonant counterpoint algorithm”:

… is a special case of what the composer and theorist Charles Ames calls “statistical feedback”: the current outcome depends in some non-deterministic way upon previous outcomes. Tenney’s algorithm is an elegant, compositionally-motivated solution to this significant, if subtle compositional idea. (Polansky, Barnett and Winter 2010)

In effect, Tenney implemented statistical feedback (the notion that past selections influence or weight probabilities for the current selection) as a means to control and modulate the short-term appearance of randomness rather than be beholden to uniform probability distributions that only appear random across large data sets or numerous actualized cases. Given the priority of time in music, Tenney’s use of a computational approach that prioritizes apparent randomness over real randomness is a subtly ingenious way to make a choice that defers choices to an automated process that, nevertheless, addresses a central compositional concern across all output values.

It is important to draw a distinction here between computer-aided algorithmic composition (CAAC), in which small tasks are given to computer programs to automate in support of a human composer, and fully algorithmic composition, in which “techniques, languages or tools to computationally encode human musical creativity or automatically carry out creative compositional tasks with minimal or no human intervention” are the focus (Fernández and Vico 2013, 515–516). I am not interested in reducing compositional choice to one’s choice of a model of artificial intelligence, nor was Tenney, I suspect. Rather, by (re)considering how a computer can aid a human composer in making choices, I think the human composer’s treatment of both functional and moral obligations remains both interesting and complex. When we have fully realized an artificial musical intelligence, the territory will irrevocably shift. But until then, the imperatives governing human artistic choice remain critical in choosing what kinds of musical decisions to automate — robust territory indeed.

Tenney’s dissonant counterpoint algorithm is an incredibly powerful, though generic, tool for CAAC. When applied in a pervasive manner (at the discretion of a human composer) the algorithm reflects a macro-level compositional choice, the semblance of which only appears as the Gestalt of its micro-level effects. Such pervasive application, even our consideration of it, highlights how simple and generic CAAC tools can be used to alleviate the burden of a human composer needing to make all choices for a given piece of music, while providing the composer with an opportunity to address the determination of music at higher levels of abstraction. Such an opportunity affords the composer time for more concerted evaluation of which choices to make, as a matter of actualized possibility or invented, radical departure. The opportunity afforded by delegation is echoed by Nancarrow, when he describes the benefit of canon: “When you use canon, you are repeating the same thing melodically, so you don’t have to think about it, and you can concern yourself more with temporal aspects” (Reynolds 1984). To this end, I propose a very general technique for automated musical decision-making: rules governing the convergence and divergence of sets of numeric data.

Convergence and Divergence of Set

In 2010, I devised and began using a particular dice game as a means to automate low-level compositional choices by deterministically changing the die that I throw to indeterminately change the appearance of sound materials. To begin to this dice game in more formal detail, I’ll first describe the software implementation of the process using a real (i.e. physical) die. Subsequently, I will describe some details of my own software implementation of this behaviour.

Given a particular die, we identify a number of pre-given cases or potentialities corresponding to the faces of the die. When we roll the die, a particular case is selected according to an (assumedly) uniform probability of selection, whereby all potential cases have an equal chance of being selected. Let us arbitrarily say that we have a six-sided die, so we have six potential cases. Each case is associated with numeric values: 1, 2, 3, 4, 5 and 6, respectively. The proposed game unfolds in the following way:

1. Determine a numeric step value (SV) that is equal to 1 divided by some integer that is greater than or equal to 1 (for instance, 1/10 = 0.1).
2. Roll the die to determine a selected case (SC).
3. Record the associated value (AV) of the SC and store it as the target value (TV) for each of the die’s potential cases.
4. Roll the die to determine an SC.
5. Apply the AV of the SC determined in step 4 to a parameter of sound generation.
6. Update the AV in one of the following two ways:
1. if the TV is greater than the AV, then add the SV to the AV.
2. if the TV is less than the AV, then subtract the SV from the AV.
7. Change the die so that the numeric result of the previous step will be the new AV for the SC on any future rolls.
8. If not all AVs equal the TV, return to step 4.

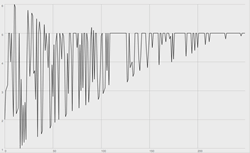
This procedure results in very specific behaviour. The die is initially governed by chance — the equal probability of selecting different cases (which we may refer to orthographically as: one, two, three, four, five and six). Each case is associated with different integer values (which we may define numerically as 1, 2, 3, 4, 5 and 6, respectively). However, after successive rolls, the value associated with each case progresses toward a consistent value outcome, the product of our first roll, i.e. the target value (TV). The more we play the game, the more the values converge toward the TV — until finally all associated values (AVs) are the same; the associated value equals the TV for all cases.

To provide an example using the aforementioned die, let’s say we roll the die and select five. We then set 5 as our TV. We then roll again and select six and then apply 6 to some parameter controlling sound generation. We then update 6 by subtracting (following step 6.ii) 0.1 from 6, which gives us 5.9. We then change the die so that the die’s sixth face (case six) has an associated value of 5.9. As we continue to roll, we select cases at random (by chance) and in each instance update the values associated with the selected case and then change the die accordingly. Eventually, cases one through six all have an associated value of 5. At this point, any die roll will yield a consistent outcome even though that very outcome was itself determined by chance. See Figure 1 for a graphical representation of value outcomes determined by 250 iterations of this exact dice game.

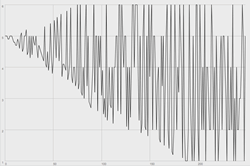
If we stop here, our game is over (or it otherwise goes on for an infinite amount of time yielding the same result: 5). However, once we have converged we may then invert the process described in step 6 (adding or subtracting the step value to or from the target value), and begin to diverge back toward the original values. Accordingly, rather than updating the selected case’s value as a means of approaching consistency, we update it in the other direction and approach randomness. See Figure 2 for a graphical representation of divergence within the bounds of the dice game described above.

Software Implementation

In software, the game is played using data structures rather than dice; an array of indexed values may function as a die. Our array constitutes a pre-given set of differentiated values — a set being a finite configuration of potentialities subject to probabilistic logic. To roll our die in software, we randomly select a value at a given “index”, which will replace the term “case” for the remainder of this paper.

In the SuperCollider programming environment, I implemented a Class Extension called “ConvergentArray” that functions like the die described above, with a few notable modifications and extensions, outlined below. 6[6. The software is currently available for download on the “software” page of the author’s website.]

Statistical Feedback Modification

The ConvergentArray object implements James Tenney’s dissonant counterpoint algorithm mentioned above, and described in Polansky, Barnett and Winter (2011). True randomness, even computational pseudo-randomness, is notoriously bumpy. For our purposes, the appearance of randomness is the priority, so I have taken pains to smooth it out: the outcomes of previous selections (history) are taken into account such that more recently selected indices are less likely to be selected and less recently selected indices are more likely to be selected. Statistical feedback biases the algorithm toward the exhaustion of the set of indices, if not series and pattern, depending on how the biasing is biased (how previously selected indices increase in their probability of selection across successive rolls).

Growth Function Modification

In the SuperCollider implementation, I further extended control over the rate and shape of convergence. The rate of convergence concerns the number of iterations (die rolls) until all associated values equal the target value. The rate of convergence is controlled by a numerical argument that we may call the number of steps. The number of steps is a constant passed to each instance of ConvergentArray upon instantiation that determines how many incremental additions or subtractions (steps) must occur for each initial associated value to reach the target value: fewer steps makes for faster, more abrupt convergence.

The number of steps is a critical value for computing not just the rate of convergence, but also the shape of convergence. The shape of convergence concerns the adjustability of the increment or step value added to, or subtracted from, the value at a given index (associated value). To refer back to our dice game analogy, we should consider step 1 in greater detail. In step 1 we calculated a step value of 0.1 in the following way: we divided 1 (which is the smallest difference between any two values in the set of all associated values) by some integer greater than or equal to 1, for which we arbitrarily chose 10. In fact, 10 served as an arbitrary value for the number of steps to reach the target value. We may, therefore, formalize our calculation in step 1 by providing the following generalized equation for the step value (v_s):

v_s = 1/N

where N is a constant representing the total number of steps to reach a target value that is ±1 from the initial associated value of a given index.

In step 6 of our dice game analogy, where we update the associated value of the selected index in the direction of the target value, v_s does not change; only its sign changes (as a matter of addition or subtraction) relative to the target value. We may, therefore, consider the above equation as a parameter of the growth function that specifies how all associated values are to be updated. The growth function described by our dice game analogy can be written in the following way:

f(x_i) = n_i × 1/N × ((T – x_i) / |T – x_i|) + x_i

where x_i is the initial associated value of index i, T is a constant representing the target value, and n_i is the number of times index i has been selected where 0 ≤ n_i ≤ N(|T – x_i|). Essentially, we multiply the v_s by the number of times the given index has been selected (n_i). This product (either positive or negative, depending on whether T is greater than or less than x_i) is added to the value at index i(x_i). The growth function may be simplified thusly:

f(x_i) = (n_i^a(T – x_i) / N(|T – x_i|)) + x_i

We should notice here how the constant N does not ensure that the target value is reached in N number of steps for all associated values (x_i). In fact, N is only the actual number of steps when T – x_i = –1, 1. If T = 5 and x_i = 3, then index i would need to be selected 20 times for x_i to reach T if we maintain that N = 10. To exert more control over the rate of convergence for the set of all associated values, we must change the growth function such that x_i for all i converge to T in N number of steps.

In the SuperCollider implementation, the growth function is changed accordingly; v_s varies proportionally with the difference between T and x_i, such that the number of times that i must be selected (n_i) for any associated value (x_i) to reach the target value (T) equals N for all i. In other words, any given index will have converged once n_i equals N. Accordingly, n_i, while necessarily greater than 0, is now bound on the upper end by N. This new growth function, the one that I have implemented in SuperCollider, looks like this:

f(x_i) = (n_i^a (T – x_i) / N^α) + x_i

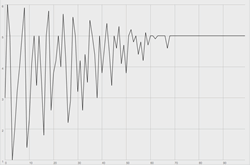
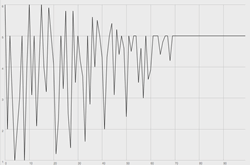
where N is any integer, T is any rational number, and n_i is any integer between 0 and N inclusive. This function ensures that N establishes a universal rate of convergence, which we may define at the outset. The shape of convergence is described by the curvature of the growth function; f(x_i) approaches T at a rate that is inflected by an exponential factor (α). A linear path toward convergence is defined by a power of 1 (α = 1), while some power greater than 1 defines an exponential path, and a power that is a fraction of 1 defines a logarithmic path. See Figures 3–5 for graphs depicting outcome values generated using ConvergentArray with an exponential factor (α) of 1, 2 and 0.5, respectively. An array of integer values [1, 2, 3, 4, 5, 6] was used in order to provide a basis for growth function comparison with the preceding graphical representations of the dice game analogy. All graphs converge to the value 5. This value was set artificially in order to further facilitate comparison.

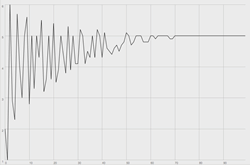
Additional Modifications

It is also important to note that the ConvergentArray algorithm operates upon sets of rational numbers. Furthermore, decimals may be rounded upon output from the growth function according to a user-specified quantization level that is defined upon instantiation. In this way, computation proceeds with full decimal precision while allowing the user to determine if the resultant values need to be more or less exact.

All of the features implemented in the CovergentArray SuperCollider class also function in reverse, as a means to diverge the given value set. By simply counting backwards (from N to 0) the number of times a particular index is selected (n_i), a converged value set can be shown to diverge by using the same growth function. Accordingly, an infinite number of iterations (of converging and then diverging) may ensue and an infinite number of computational modifications may be brought to bear on the parameters governing such behaviour. Figure 6 provides a graph of a divergent trajectory and may be considered an inversion of the convergent trajectory shown in Figure 3.

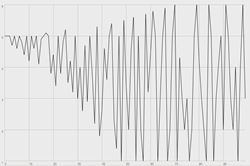
Based on the behaviour of the algorithm and the modifications discussed here, our ability to control a variety of parameters raises many questions about “how”, “when” and “within what bounds” we move to mathematically converge and diverge value sets. It is through our consideration of how the growth function changes values applied to sound synthesis that we encounter a multidimensional territory of possible change.

Applying ConvergentArray

Once implemented, ConvergentArray is primed to modulate the parameters of sound synthesis in a way that is neither completely predictable nor wholly chaotic. The way that I have sought to implement such functionality is to instantiate a new array for each defined parameter governing sound synthesis. Take, for example, the generation of a simple sine tone. Immediately we may want to control the sine tone’s frequency and its amplitude. My response to this situation is to instantiate two ConvergentArrays, one that governs the frequency of the sine tone and the other the amplitude. Each parameter is thereby left to converge and diverge according to its own set of values, number of steps and growth function exponent. Furthermore, each ConvergentArray may be updated with a new set of values independently (this is usually best to do at a point of full convergence or full divergence).

If we imagine a sample-based instrument or instruments with dozens of parameters, with each parameter being modulated according to a ConvergentArray, the set of possible appearances of the resultant sound is vast. If we then multiply the number of running instances of such ConverventArray-controlled instruments, signal (tracking any one convergent or divergent trajectory) becomes lost and data-driven noise reigns supreme. As a result of potentially multiple convergent and divergent processes running at the same time, aural appearances may shift in seemingly infinite ways — and not just as a matter of indeterminate selection, but rather, as the seemingly miraculous emergence and disappearance of some telos. As outcomes veer toward and away from consistency, momentary directionality is called into question.

Conclusion

When implemented pervasively and hierarchically, the ConvergentArray algorithm can generate incredibly varied sonic configurations that instigate composer choice within two key domains: to navigate around core perceptual issues regarding the accumulation or decumulation of sound materials and to invent new possibilities for the treatment of, and interpolation between, regular and irregular sonic configurations. Directionality, perhaps most directly associated with functional harmony and cadential motion, here becomes addressable as an abstract procedure of successive die rolls. It is precisely the generic, non-domain-specific, or “unintelligent” nature of this technique for automated musical decision-making that allows a composer’s deferral of choice to the algorithm to become an opportunity for thoughtful consideration of the functional and moral obligations that condition higher order choices taking place. Given the development of such a selection tool, and its ability to limit and reconfigure options, it is now incumbent upon us to ask: “What would happen if…?”

Bibliography

Badiou, Alain. Theoretical Writings. Edited and translated by Ray Brassier and Alberto Toscano. London: Continuum, 2004.

Bivins, Thomas H. “Responsibility and Accountability.” Ethics in Public Relations: Responsible advocacy. Thousand Oaks CA: Sage Publications, 2006.

Brün, Herbert. When Music Resist Meaning: The major writings of Herbert Brün. Edited by Arun Chandra. Middletown CT: Wesleyan University Press, 2004.

Cage, John and Daniel Charles. For the Birds: John Cage in conversation with Daniel Charles. Edited by Tom Gora and John Cage. London: Marion Boyars, 1981.

de Certeau, Michel. The Practice of Everyday Life. Trans. Steven Rendall. Berkeley CA: University of California Press, 1984.

Fernández, Jose David and Francisco Vico. “AI Methods in Algorithmic Composition: A Comprehensive survey.” Journal of Artificial Intelligence Research 48 (2013), pp. 513–582.

Kablat-Zinn, Jon. Everywhere You Go, There You Are: Mindfulness meditation in everyday life. New York: Hyperion, 1994.

Polansky, Larry, Alex Barnett and Michael Winter. “A Few More Words About James Tenney: Dissonant counterpoint and statistical feedback.” Journal of Mathematics and Music 5/3 (2011), pp. 63–82.

Reese, Byron. “Interview with Stephen Wolfram on AI and the Future.” GIGAOM. 27 July 2015. http://gigaom.com/2015/07/27/interview-with-stephen-wolfram-on-ai-and-the-future [Last accessed 4 November 2016].

Reynolds, Roger. “Nancarrow: Interviews in Mexico City and San Francisco.” American Music 2/2 (Summer 1984), pp. 1–24.

Schwartz, Barry. The Paradox of Choice: Why more is less. New York: HarperCollins, 2004.

Tuan, Yi-Fu. Space and Place: The perspective of experience. Minneapolis MN: University of Minnesota Press, 1977.

Žižek, Slavoj. Less Than Nothing: Hegel and the shadow of dialectical materialism. London: Verso, 2012.