Combinatorics, Probabilities and Personal Big Data in the Sound Installation “P(N,R) = N!/(N-R)!”
Big Data, Personal Big Data: An Introduction
Big data, wide data, fast data — we hear and read these words every day in a variety of contexts, from tech blogs to radio shows. But what is the size, pace and rhythm of such a flow and accumulation of data? Size is critical: are we even capable of actually grasping the size of such emerging concepts? And what of the size of the data that we accumulate over the years as artists, as composers in the digital age: audio files, patches, sequences, stems, mastered tracks and various mixes, not to mention multiple backups of all of the above…
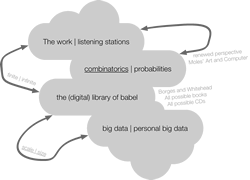
Broadly inspired by these open-ended questions, we created a miniature sound installation for the specific context of Centre Clark’s Poste Audio in Montréal in 2015. The piece was subsequently presented in the Sines and Squares festival in Manchester (18–20 November 2016) as well as in the Complex Interactions Exhibition hosted by NAISA — New Adventures in Sound Art (South River, Ontario, Canada, 29 June – 4 September 2017). While creating this miniature sound installation as an interpretive form of the formerly ubiquitous listening stations, we were thinking of these data-related themes in parallel with combinatorics within a wider perspective. The landscape of these connected themes can be represented as a cloud of topics (Fig. 1) through which the present text will freely navigate, guiding us toward the idea of personal big data.
P(N,R) = N!/(N-R)! — The Work and the Listening Stations
When we were invited to produce one of the editions of Poste Audio at Centre Clark in Montréal, we were first dealing with the specificity of the context. Centre Clark is an artist-run centre comprising two gallery spaces. Just inside the entrance, there is a listening station known as the Poste Audio that was, in 2015, curated by Sébastien Cliche. Sometimes, specific works are created for the Poste Audio. In our case, we were interested in the listening station as an historical cultural object that was found in every record shop throughout the CD era. Accordingly, we decided to create a listening station as a sound installation. Our conceptual focus was then to explore the listening station from the perspective of headphones-based spatial audio and with a focus on the visitor’s will and selection of headphones.

The installation was first presented at Centre Clark in September 2015 (Fig. 2) with six single-cup headphones on a dedicated table. These headphones were connected to three Raspberry Pis running a total of six command-line audio players. The setup was therefore comprised of six media players, and the visitor would select two (or one) of the six available headphone cups — i.e. the installation includes N headsets with R selected at any given time by the present user. This design was selected as a way of encouraging the individual listener’s act of selection and spatial composition from a large number of audio files and sound compositions. With respect to the actual sounds, our starting point was the idea of the artist studio as a place where visitors can shift the focus of their attention at will — a place that combines raw materials, unfinished works, finished works, notes and sketches and ideas in a range of unplanned and unforeseeable juxtapositions. To transpose this idea into the realm of sound, we recorded all of our improvisations on modular synthesizers — including the sounds resulting from patching and “unpatching” the units — for a period of eight months. The strategy was then to collect and accumulate sounds, performances and audio data, without subjecting it to a process of selection, as a first move toward the establishment of a body of sound data whose size existed at the composer or artist scale.
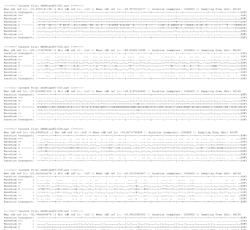
In the course of making the work, we accumulated approximately 10 GB of recordings, corresponding to approximately 15 hours of a mixture of short (1 second) to long (60 minutes) audio files. To explore this as data and as data accumulation, a simple Python script was created to load the audio files, perform simple data extraction and export their waveforms, displayed as ASCII-based text (Fig. 3). The Raspberry Pis were then each equipped with a 12 GB USB stick and a simple script was used for the playback of contents from audio folders. The corresponding ASCII “scores” generated from the Centre Clark installation were shown alongside the work when it was exhibited by NAISA in 2017.
The Listening Station, the Record Store and the Library as Cultural Objects
As a first exploration of data size using numbers, let’s consider the former record store as a finite container of fixed-size data supports: CD, floppy and hard disks, and tapes. The record shop as a library, or as a bookstore — a finite container of finite-size data supports, books, magazines and newspapers. This will later on connect us to Borges’ Library of Babel. Our first speculative question is, what would the size be of a record store corresponding to a 1 TB hard drive full of MP3s? According to a rough approximation based on the average size of a song stored as an MP3, 1 TB should correspond to 250,000 MP3s or 25,000 albums, assuming an average of 10 pieces per album (based on an average pop music release). Taking a look at the spine of a standard single-CD jewel case — as it would be seen in rows in most record shops — we see that it occupies 0.012896 m2 (1 x 12.5 cm). So, in the case of 25,000 albums, we can assume a total shelf area of just under 31.25 m2 (25,000 x 0.00125 = 31.25 m2) would be needed — a number that remains at the human scale. The listening stations managed by the owner and employees of such record stores offered a means to quickly navigate through “curated” selections from an enormous amount of music and this developed into the cultural practice of listening before purchasing. These specific listening practices and habits have now been transposed to online music searches and purchases.
Probabilities, Combinations
As mentioned, the installation was offered as a selection process from the perspective of the visitor. This motivated the title of the work, P(N,R) = N!/(N-R)!. We were interested in a title that pointed to probabilities and combinations. The title should be read and decoded as follows from a mathematical perspective: P(N,R) is the number of possible permutations as a function of N and R: N is the number of possible choices, while R is the number of items selected at a given time. In mathematics, the exclamation mark denotes the “factorial” operation: N! is interpreted as N x (N-1) x … x 1. For instance:
4! = 4 x 3 x 2 x 1 = 24
We selected this simple known permutation equation as part of the title to reflect the fact that the composition was left a set of possible permutations in the hands of the visitor. For the specific case of this piece, one finds N = 6 and R = 2 (i.e. a choice of 6 players and 2 headphone cups at any given time). So for two-channel listening in this context, N!(N-R)! gives 30 possible permutations (6!/4!), and for single-channel listening one obviously finds 6 permutations, offering a total of 36 possible channel permutations from the listener’s perspective. This may seem like a limited set of combinations, but, when combined with the 10 GB of audio files and the massive number of combinations the six independently running playlists can generate, the number of potential combinations drastically increases. Nevertheless, the title was chosen above all to suggest the idea of combination rather than as an exact prediction of all possible combinations.
Combinatorics in Music and Arts
A Few Words
Moving back to a more general or historical perspective on combinatorics in music and arts, permutations and combinations are obviously not a new idea. Many scholars and composers have already been writing on this topic with much more in-depth considerations. From serialism, dodecaphonism, tone row matrices to John Cage, combinatorics and processes were, for some but not all, a potential strategy to challenge the concept of the artist as a genius or romantic figure. That being said, we will not explore further into this already well-documented topic and line of thought. Instead, we will attempt to shed light on this question and corresponding work from another, perhaps less known, perspective offered by Abraham Moles.
Abraham Moles: Art and Computer
In 1971, Moles published Art et ordinateur [Art and Computer], a fascinating and forward-thinking book. If this book can be criticized for being deterministic or grounded in mathematics, it remains a very inspiring and visionary work that explores art as a multiple or as permutations.
Starting from Benjamin’s Work in the Age of Mechanical Reproduction, Moles suggests a historical move toward permutational art with the computer age (Moles 1971). For instance, he highlights the fact that multiple versions of the same work of art created using mechanical reproduction were actually not all the same. They presented random yet subliminal (in the literate or scientific sense of being under the perception threshold) variations from a normative form. As an example, let us consider printing as one normative form. Even if prints were mass-produced, tolerance in machinery and printing processes typically lead to subliminal variations or permutations. Another sound-related example is the normative form of vinyl records. For a given album, each copy from the same pressing sounded the same, but the background noise and imperfections inherent to the medium lead to subliminal variations or permutations of the normative form. From this historical perspective, Moles takes this kind of variation as a differentiating feature of computer art: variations or permutations should no longer be considered subliminal but rather central to future computer arts in which algorithmic procedure is identified as a key element or even as the work itself — one of many new ways to explore a vast span of possibilities. In our view, computer aside, this is one of the richest theoretical frameworks for P(N,R) = N!/(N-R)!.
Permutational art suggests a homogeneous field of possibilities, can contribute to the creation of monumental conceptual objects and can be a conceptual work that suggests infinity.
According to Moles’ ideas as presented in Art et ordinateur, permutational art is essentially based on elements and assembly. The artists pick the elements and select a combinatorics algorithm. The elements will be perceived as reflecting the artist’s sensual or æsthetic taste. For our installation, this was manifest in our decision to exclusively use sound elements that were derived from modular synthesizers. The selected algorithm then works to produce a field of possibilities. Typically, as suggested by Moles, the algorithm is managed by the duo formed by the artist and computer. Or, in some cases, it is also possible to leave some decisions regarding elements or algorithmic procedures for the visitor or listener to make while experiencing the work — this the case for P(N,R) = N!/(N-R)!. Within the range of possible algorithms, he mentions permutation, arrangement, combination (here it is good to recall that the book is from 1971) and the corresponding equations in terms of possibilities and variation. Moles aptly shows that the number of possible assemblies is vast even for a limited set of elements. Besides this, he provides interesting ideas to explain the potential artistic meanings of permutation in art. Three of them are relevant for us. First, permutational art is a way to suggest a homogeneous field of possibilities from a set of elements. Second, it can contribute to the creation of monumental conceptual objects. Third, the author suggests that a permutational work can be a conceptual work that does not provide all the possible combinations but that rather suggests infinity.
In this vein, Moles provides examples from literature such as permutational poems that are literally impossible to grasp and leave a sense of monumentality, if not infiniteness. Therefore, Moles relates permutation in art to size and conceptual vastness. He cites a few historical examples, such as Quirinus Kuhlmann, who in 1671 created a conceptual object of 1047 incomplete poems based on the 50 words of the original poem. This speculative work is incomplete, as the combinations have not been written, per se. Here the mere suggestion of the process is the work. Another refreshing perspective is found in Sade’s 120 journées de Sodome, which is better known for its sexual violence than its mathematical contributions. However, as Moles suggests, this work can also be seen from a combinatorics perspective: starting from elements such as humans, organs, body parts, fluids and ingredients, Sade offers a literate and structured exploration of all their possible combinations. Indeed, this particular work by Sade often leaves a strong impression of a documentation or an inventory of the possible combinations of elements.
In addition to ideas of dimension and infinite combinations of elements through algorithmic procedures, Moles also suggests that some of the permutational works that leave the combining tasks in the hands of the visitor directly address the idea of communication. In the sense that discovering a piece, from the visitor’s perspective, means trying to exhaust the work — a rather futile task, given that the vastness of combinations is beyond human scale or available time.
In the end, Moles’ point is that permutations and combinations can provide a feeling of the infinite through a finite set of elements or processes, where infinite is thought of in a perceptual sense — it goes beyond perception or even conceptualization. And from that point, we reconnect this idea to the aforementioned topic of size, previously exemplified for the case of the defunct record shop and its listening stations. In the following section we expand this concept to The (Digital) Library of Babel and to the hard drive.
Data and Data Size: A Few Case Studies
The Library of Babel
Jorge Luis Borges wrote The Library of Babel (La biblioteca de Babel) as part of Fictions, which was published in French by Folio in 1983 and originally dated from 1944. As an Argentinian author, Borges contributed to philosophical and fantasy literature through works often identified with magical realism. In his writing, one always finds a conceptual twist that mixes modernism, mathematics and philosophy. Here, we focus on the popular Library of Babel as a brilliant short story about all the imaginable literature derived from a finite set of letters.
Borges describes his Library as a series of hexagonal adjacent rooms with four walls made of bookshelves; the remaining walls connect to other rooms. The order and content of the books are apparently random — from the perspective of “librarians”. All books contained within the Library are based on the same 25 characters or letters. Accordingly, this “infinite library” of all possible combinations of letters should contain everything from random nonsensical texts through to the greatest masterpieces… in parts, combined or with errors, and including its author’s own text. Part of Borges’ fiction is about the potential reaction of the librarians facing this literature collection as an object or as a universe. For the users facing this vastness of “all textual information” (which includes truth as well as information garbage) a gradient of reactions is possible. Some librarians fall into superstition schemes, cults and other theories. For instance, some librarians mention that locating meaningful Books is an infinite task and therefore it might not make sense to even begin to mine the Library. Borges’ conceptual and philosophical work introduces a simple question: How should we deal with the vast amount of information derived from infinite combinations? In his words and from a critical perspective: “The infinite storehouse of information is a hindrance and a distraction because it lures one away from writing one’s own book (i.e., living one’s own life).” We will not debate here the value of this interpretation, but will rather focus on the conceptual object of the library, seen from a digital perspective.
The (Digital) Library of Babel
In 2012, James Whitehead actually conceived of a digital adaptation of The Library of Babel. In Two Experiments, Whitehead proposes a philosophical exploration of noise in music. He aims to show that “noise has an ‘objectivity’” and, further, that “Particular noise works exhibit properties or a lack of properties that enable these works to be regarded as things in themselves.” To do so, Whitehead partly relies on the study of the compact disc from a mathematical perspective using an extension of Borges’ The Library of Babel. Whitehead’s theoretical speculation is related to our topic with respect to data and data size as an interesting thinkable object in relation to permutation and combinatorics.
The CD is interesting because it is the most recent commodified physical object of “recorded sound” (ignoring MP3 players and hard drives for the moment). It is the last physical object of musical sound data before the advent of online P2P, MP3 and portable players. Let’s imagine a collection that contains all possible CDs. On a single, standard CD, one finds:
- Two channels;
- A maximum duration of 74 minutes;
- 60 seconds per minute;
- 44,100 samples per second;
- 16 bits per sample.
Accordingly, we find that 2 x 74 x 60 x 44,100 x 16 is equal to 626,572,800 bits, or 740 Megabytes. This is a standardized finite size of data. Based on that finite size, what is the number of all possible CDs that would include all possible 2-channel sound (whether music, noise, voice or other) of 74 minutes (total duration)? To find it, we have to know that for a pack of n bits (each corresponding to 0 or 1), there are 2n possible n-bit words. For instance, for n=2, we could have 00, 01, 10, 11, i.e. 22=4 possibilities. For black and white images described by 8 bits, we have 28=256 possible shades of grey. So, for our case, we find the answer to the previous question expressed as a power: 2626572800, i.e. 2 multiplied by 2 repeated 626,572,800 times. This is not infinity, since we start with a finite size. However, from a human perspective, this surely feels like infinity.
Back to Whitehead’s text. He aptly notes that the number of physical objects is not equal to the number of possible experiences involving those objects. In the case of the CD, it also depends on the interpretation of the 0s and 1s: are they sounds, images, ASCII texts? The set of all possible CDs is based on random, yet exhaustive, combinations of 0s and 1s. We can imagine a library or a record shop containing all possible CDs — but that would be equivalent to noise, with sparks of music and of existing or future works. All possible sounds and voices, existing or yet unknown. The fascination for this idea of all possible noises and all possible music in a single finite set is perhaps the most important part of the argument. Although it would be possible to evaluate the size of the record store that could house all CDs, it would only provide a number larger than 2626572800. If the idea of all CDs already goes beyond and reach the desired vertigo as evoked by Moles, what about more recent formats and data containers?
From the Compact Disc to the Personal Hard Drive

In the 1990s and at the beginning of the 2000s, the hard drive was the ubiquitous data container for our personal and digital lives. Mathematical evaluation of the size of permutation is more challenging in this case. We cannot even think of a number since hard drives are of finite size, yet they increase in size constantly. Perhaps the question of size should then take a more conceptual form: What is the size of our artistic lives and production rates as composers, musicians, artists in the digital era?
Turning to our personal situation, we checked one of our laptops dedicated to sound works. We found just over 70 GB of sound (38 + 33 in 2 separate locations) on the SSD-based laptop we have been using in the past few years. This corresponds roughly to 105 hours of sound from a set of 206.7 GB of data (see Fig. 4 for an analysis of our hard drive content). This was surprisingly less than expected! Some reflections from the perspective of personal big data will offer a glimpse into the cloud age of big data.
Big Data and Personal Big Data
The Unimaginable Size of Big Data in the Cloud
Tung-Hui Hu recently published a fascinating book titled A Prehistory of the Cloud (2015). Tracing back to the idea of users in computer networks and to railroad infrastructures, Hu shows how the cloud is actually a material machine. Currently, personal hard drives are used, but the cloud storage of data is occupying more and more physical space; with mobile phones, it is actually increasing at an astonishing pace.
As mentioned by Hu, the Cloud is often said to have arrived in our lives in 2010 or 2011. However, ideas of grid of computers can be traced back to 1922 by AT&T and then Electronic Skyway. It is interesting to see that the image of the cloud was originally a simple schematic symbol used in technical drawings. It was used to identify a network that may fluctuate in size and type with heterogeneous components. Therefore, we cannot easily separate the Cloud from a historical lineage of networks, including informatics, electricity and even mechanics and pipes (Hu 2015).
As our preferred storage devices changed from CD to hard drive to the Cloud, the question of the extent and size of possible permutations is now lost in infinity. Although it cannot be infinite per se, since the original data size is still of finite size. The problem is, however, the fact that we are now conceptually dealing with moving or undefined boundaries of that finite size. Thus, what is the most accurate about the word “cloud” in informational technologies is not its illusory immateriality but rather its expandable and blurry boundaries. In this context, size and technological heterogeneity of storage no longer matter, at least from the individual user’s perspective. Size, and possible combinations, is cost, material and infrastructure… but vaporized from our personal, individual, user’s point of view. Then, the question remains: What is the size of a personal life in the digital era?
From Big Data to Human-Scale Big Data
Perhaps this last question is trivial, as the size of personal digital life can only grow exponentially. Turning our focus back to our modest 10 GB of sound data derived from 6 months of various unstructured improvisations, is it possible to conceive of a human-scale big data set, or a personal big data set, that already affords a vast number of combinations? Neither the creators of P(N,R) = N!/(N-R)! nor the various listeners or visitors that have experienced this noisy combinatorial device have ever heard all the possible combinations of playback timing, sound files and headsets for the work.
Let us consider the path we have taken here. We started with reflections on the size of a record store or a library replete with listening stations, interactions, human choices and combinations, before pondering the size of The (Digital) Library of Babel and the storage capacity of today’s hard drives and finally on to the ungraspable size and combinatorics of the Cloud. Can we even imagine the scale of an Abraham Moles’ example of all possible work in that context? If Borges asks questions related to the span of possible reactions to this information vertigo, including the desire to search for ultimate meaning from within a garbage heap of data, he also insists on the fact that such an enterprise (not so dissimilar to the fantasy of data mining) can lure one away from writing one’s own book. P(N,R) = N!/(N-R)! was our own modest book. We now plan to work on something between personal data, big data and data mining.
Postlude
In 2013, the size of the Internet was evaluated as the equivalent of 1200 petabytes, which corresponds to 1.2 million connected and switchable terabytes (Mitchell 2013).
Acknowledgments
The authors would like to thank Sébastien Cliche for the initial invitation to present this work in Centre Clark’s Poste Audio project. We also acknowledge the contributions of Centre Clark, where the actual table was specially designed for the piece. The Conseil des arts et des lettres du Québec is also acknowledged for supporting our training during the Sines and Squares workshops in 2016. Finally, Darren Copeland and NAISA receive warm thanks for presenting the piece in 2017.
Bibliography
Borges, Jorge Luis. Fictions. Trans. Roger Caillois, Nestor Ibarra and Paul Verdevoye. Paris: Gallimard, 1983.
Hu, Tung-Hui. A Prehistory of the Cloud. Cambridge MA: MIT Press, 2015.
Mitchell, Gareth. “How Much Data Is on the Internet?” 23 January 2003. http://www.sciencefocus.com/qa/how-many-terabytes-data-are-internet [Last accessed 25 February 2018].
Moles, Abraham. Art et ordinateur. Paris: Casterman, 1971.
Whitehead, James. “Two Experiments.” Tacet — Experimental Music Review 2 (2012) “Experimentation in Question,” pp. 284–315.
Social top