Symbolic Representation of Chords for Rule-Based Evaluation of Tonal Progressions

by Eddy K.M. Chong and Qin Ding

Modelling Tonal Harmony

The grammar of music harmony has a complexity that defies simple computational representation and that has certainly engaged the imagination of music theorists for centuries. This project is concerned with the computational representation of harmonic grammatical rules of the eighteenth- and early nineteenth-century for teaching purposes. Broadly speaking, in music computational endeavours, two directions have been explored — either to model after human music-theoretic thinking or to aim for an output capability that is comparable to human efforts, even if the system is musically naive or its “musical thinking” is opaque to the system designer. Both approaches have their pros and cons. For us, the ultimate objective is a pedagogical one, therefore we chose the former.

More specifically, we align our research with common musical understanding in order to develop an interactive system that not only evaluates the validity of chord progressions in the manner of a trained musician, but also offers automated error feedback to the user, similar to that given by a music theory teacher. The knowledge base of this AI system — from its data encoding to the declarative rules and constraints implemented — is therefore necessarily grounded in one of the current standard harmonic theories, in this case, as taught by Eddy Chong in an undergraduate music theory course (akin to Laitz 2012 and Roig-Francolí 2011). Whilst it may be argued that a computational model based on statistical comparison of patterns or structures may yield viable sets of rules, these are unlikely to match the important details central to the theory that is taught in our case; this will be made clear below.

Within the confines of this paper, we shall present in more detail the symbolic representation system, and only sketch out and briefly illustrate our rule-based system for evaluating harmonic progressions.

Input Data

In designing the evaluation sub-task, we first need to choose the type of input to work with. Given that music is a sound-based art, one would expect that from a human-and-sound interaction point of view, the preferred input would be sonic in nature. Indeed, there have been quite a number of such precedents (Conklin 2002; Dixon 2010; Mauch and Dixon 2010; Mauch, Noland and Dixon 2009). However, our pedagogical intention is to help students master the basic principles of functional tonal (but not modal) harmony, expressed in Roman numeral and voice-leading terms. Hence, we have chosen not to have students use audio input (e.g., playing the progression on a MIDI keyboard or recording the progression through other means) or even music score notation, but to input using the Roman numeral system taught in class, one which in later stages can be applied to more elaborate voice-leading situations such as those shown in Figure 1. Of course, for future developments of the system, we can add a conversion component to accept alternative “raw” inputs, but our present focus is to develop the evaluative function itself, which is the “cognitive” core of the system.

By opting for the abstract form of Roman numerals, we are also simplifying the overall computational task by eliminating the need to handle non-harmonic tones, a complication that a number of researchers have chosen to tackle based on their differing motivations but only succeeded to a limited extent (Harte et al. 2005; Mauch 2010; Maxwell 1992; Sapp 2007; Winograd 1968). At the same time, we sidestep the need to deal with key-finding (unlike Maxwell 1992; Sapp 2007; Taube 1999; Winograd 1968) as well as the parsing of different types of musical texture (e.g., Maxwell 1992). Admittedly, the use of pop or Jazz chord symbols, sometimes referred to as guitar chords (e.g., in Anglade and Dixon 2008; Granroth-Wilding and Steedman 2012; Temperley and Sleator 1999), may circumvent a number of the just-mentioned computational challenges, but it still entails the additional sub-tasks of key-finding and of determining chord relationship, the two being strongly mutually dependent. As such, the Roman numeral system is still more ideal in that it allows us to be more focused in our computational development.

Now, having opted for the Roman numeral system, there is still the need to choose the particular version. In accordance with the theory that is taught in our context, our Roman numeral system differentiates between chord types, as illustrated in Table 1. This separation between major and minor key paves the way for handling borrowed or mixture harmonies for future extension of the system, which currently deals only with diatonic harmonies. We use figured-bass numbers to indicate the chord inversion — for example, “6” for first inversion, “6/4” for second, and so forth — as opposed to using suffix alphabet letters (e.g., Ib, ivc, V7d). The notion of harmonic function is also integral. Hence, cadential six-four is clearly distinguished from its other counterparts, which retain their Roman numeral. For example, I6/4 may be a neighbouring or passing six-four, but it is decidedly not a cadential six-four, which is symbolized as C6/4 in the major key, c6/4 in the minor.

Data Representation

The next step is designing the data representation system. Whilst there are quite a number of versions currently available, none of them entirely meet our pedagogical need. This is not surprising, since the suitability of any representation system depends very much on the task it is designed to serve, and it must factor in both the context of the notation itself as well as the processes that it is subject to (Wiggins et al. 1993).

In our case, the data representation must be aligned with the tonal theory that is taught. Specifically, it must reflect diatonic and chromatic relations as well as other features pertinent to harmonic voice-leading considerations. With this in mind, we adopt a four-element vector <a,b,c,d> in which “a” represents the key (1 = major, 2 = minor), “b” represents the scale degree (1 to 7), “c” represents the chord type (1 = major triad, 2 = minor triad, 3 = diminished triad) and “d” represents the chord inversion (0 = root position, 1 = first inversion, and so forth). For scale degree indications, the major-key scale step is used as a reference. Hence, in the minor key, the mediant chord is bIII and is encoded as “36”, where the second digit “6” signifies the chromatic lowering (“6” morphologically resembles the flat sign). On this basis, mixture or borrowed harmonies can be easily distinguished from their diatonic counterparts subsequently.

For seventh chords, the encoding rationale is a little more complicated. With extended major chords, a second digit “7” is added. In the context of Classical usage, whether the added seventh is a major or minor one depends on the chord in question. For example, in the major key, c = 17 will mean added major seventh in the case of I7 and IV7, but added minor seventh in the case of V7. Extended minor chords are more straightforward since only the minor seventh (c = 27) is typically added in Classical harmonies. To differentiate between full- and half-diminished seventh chords, “37” and “34” are used respectively. Additionally, we assign the cadential six-four a special category (c = 564, for both modes of the key).

With this chord encoding system, a progression would be represented as a string of vectors. For instance, the commonplace progression iiø6/5-V7-i in the minor key is encoded as <2,2,34,1>, <2,5,17,0>, <2,1,2,0>. Figure 2 illustrates our encoding system with a slightly longer progression modified from this harmonic cliché.

A Case for Declarative Rules

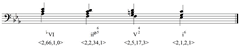
In music, harmonic grammar is either grasped intuitively by musicians or explicitly learnt, in which case intuitive processing may still be involved. To model this grammar, music computation researchers either induce such rules from a set of data (e.g., using neural network or other machine-learning methods) or adopt declarative rules based on known theory. While the statistical approach of the former may produce relevant results, we have opted for a rule-based approach for the following reasons:

1. The musical logic of “discovered” rules remains opaque, hence inductively derived rules are ill suited to provide the specific error feedback that we desire, especially one that is aligned with the theory taught here.
2. The significance of inductively derived rules is based on statistical count rather than musical consideration, so unless one is interested only in the input-output efficiency of the model, one would need to further ascertain the music-theoretical validity of the rules. In other words, frequency of occurrence and statistical significance do not automatically equate with musical significance; the latter needs to be humanly evaluated (Conklin and Anagnostopoulou 2001). For our purpose, this would be necessary — an extra task we would prefer not to bring into the project.
3. Furthermore, even if we do attempt to interpret the “discovered” rules in musical terms, it is likely to be a tedious process with limited benefits. For example, one fairly recent inductive logic experiment applied to Jazz and pop harmonies has yielded over 12,000 rules, most of which cover less than 5% of the data (Anglade and Dixon 2008) and the extent to which this whole set of rules is able to account for Jazz and pop harmonies is unclear.

Given the complex behaviour of harmonic progressions and the astronomical number of possible chord successions, no set of textbook harmony rules can fully deal with all musically acceptable progressions, even within the confines of Classical harmony. Indeed, in the process of testing the system with real musical examples, there have been instances where our initial rule system fails to accept certain less common but nonetheless acceptable progressions, or it has accepted what is normally considered undesirable progressions (but made to work by the composer): such is the complexity of harmony in its interaction with other musical parameters such as melody and texture, a phenomenon that Schenker — the great theorist who had a profound understanding of tonal harmony — recognized (Chong 2002, 39–45). In refining our rule-based system, we have therefore relied on our musical intuition to evaluate the validity of the progression where standard rules “fails”; in some cases, we made certain rules appear less dogmatic to allow for composers’ creative endeavours. By thus crafting our rules and the feedback comments, we affirm that music is fundamentally a creative product that is not entirely or strictly governed by rules. Therefore, translated pedagogically, students are taught that rules are no more than starting points of learning; they should know how to use them creatively.

Overview of the Rule-Based System

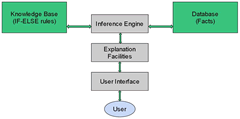
Since this paper is focused on presenting the data representation aspect, we shall merely offer here a quick overview of our rule-based system. In computer science, a rule-based system embodies knowledge that can be used to interpret information in useful ways. In artificial intelligence applications, such domain-specific expert systems emulate the decision-making ability of a human expert. Our rule-based system (Fig. 3) is based on JBoss Drools (version 6.0.0.Final), which is a Business Logic integrated and unified platform for a rule engine to operate in accordance to a particular workflow. Rete algorithm, an efficient pattern-matching algorithm, is the basis of our Drools rule engine (Forgy 1982).

Our musical rules are formulated based on considerations of root motion, bass movement and other tonal voice-leading factors. These can grow to unwieldy dimensions — especially as we move towards more advanced harmonic styles subsequently — such that the traditional approach to “if-else” algorithm will be less efficient in processing the input data. We therefore opted for a Rete approach for its more efficient decision tree structure.

There are broadly two categories of rules implemented. The first stipulates certain constraints to ensure the specific kind of harmonic progressions we wish the user to be focusing on. For example, should we make chords from parallel keys available for the user to choose from, the rule “All chords in a progression must be in the same key” limits the user to diatonic progressions, thereby allowing us to test his/her ability to distinguish between diatonic and chromatic chords. The second category pertains more specifically to harmonic voice-leading considerations. For instance, “If the current chord inversion (d) is 2 and the current nature (cx) is 564, then the next scale degree must be 5 and its d-value must be 0 or 3”; this stipulates the two common resolutions of the cadential six-four chord (Fig. 4). In this connection, if this second-inversion chord is a passing or neighbouring one, another set of rules is implemented to ensure proper voice-leading handling of this unstable harmony.

Beta Testing

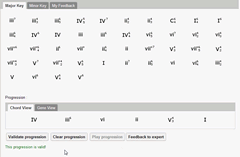
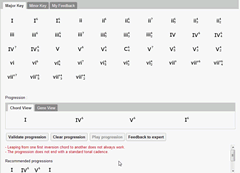
As a preliminary test, we used a number of Bach’s harmonized chorales from the Riemenschneider collection to test the system. Bach’s chorales have been a popular choice amongst music computation researchers (Conklin 2002; Ebcioğlu 1992; Kröger et al. 2008; Sapp 2007; Taube 1999; Winograd 1968). However, not all progressions from this chorale collection are suitable for testing our system, which currently deals only with diatonic progressions. Most of Bach’s harmonizations involve tonicization or transient modulations; these are excluded since we have not included applied chords in our current system, or any other chromatic harmonies for that matter. On the other hand, some of Bach’s harmonizations are modal rather than functionally tonal in nature; these then wonderfully serve to test the system’s discriminating ability within a diatonic context. Video 1 illustrates the evaluation of a stylistically correct progression and Video 2 that of an unacceptable one, with the automatic feedback that is given. In general, some of the test progressions have involved as many as ten chords. The testing was done manually by the first author and any anomalous error feedback was used to ascertain whether the set of implemented rules needed to be refined or new rules added.

Interim Evaluation and Future Work

Thus far, our system can by and large successfully evaluate progressions drawn from over 50 chorale harmonizations and provide appropriate error feedback. This includes correctly detecting modal progressions that do not conform to certain tonal functional rules. A number of faulty progressions have also been deliberately created to further test the system. The next phase of testing will involve student-created ones as well as progressions drawn from other similar-style tonal repertoire.

Once the robustness of the system is sufficiently tested, we will expand the system to embrace chromatic harmonies such as applied chords (e.g., V/V) and modal mixtures (e.g., bIII in the major key). In the longer term, other harmonic styles (e.g., pop, Jazz) can be evaluated by changing the list of chords and set of rules. In fact, the encoding system itself is flexible enough to be modified to tackle even non-triadic harmonies, with the encoding vector being shortened or extended accordingly.

Acknowledgements

We would like to thank Yu Zhenyu and Jia Ruitao for their work in the earlier phase of developing the computational model.

Bibliography

Anglade, Amélie and Simon Dixon. “Characterisation of Harmony with Inductive Logic Programming.” ISMIR 2008. Proceedings of the 9th ISMIR Conference on Music Information Retrieval (Philadelphia PA: Drexel University, 14–18 September, 2008). Available online at http://ismir2008.ismir.net/papers/ISMIR2008_189.pdf [Last accessed 6 March 2014]

Chong, Eddy K.M. “Extending Schenker’s ‘Neue Musikalische Theorien und Phantasien’: Towards a Schenkerian model for the analysis of Ravel’s music.” Unpublished PhD dissertation, Eastman School of Music, 2002.

Conklin, Darrell. “Representation and Discovery of Vertical Patterns in Music.” In Music and Artificial Intelligence. Proceedings of ICMAI 2002 — 2nd ICMAI International Conference (Edinburgh, Scotland: University of Edinburgh, 12–15 September 2002). Lecture Notes in Computer Science, Vol. 2445.

Conklin, Darrell and Christina Anagnostopoulou. “Representation and Discovery of Multiple Viewpoint Patterns.” ICMC 2001. Proceedings of the International Computer Music Conference (Havana, Cuba, 2001, 17–22 September 2001). http://finearts.uvic.ca/icmc2001/main.php3

Dixon, Simon. “Computational Modelling of Harmony.” CMMR 2010. Proceedings of the 7th International Symposium on Computer Music Modeling and Retrieval (Málaga, Spain: University of Málaga, 21–24 June 2010). Available online at http://www.eecs.qmul.ac.uk/~simond/pub/2010/Dixon-CMMR-2010.pdf [Last accessed 6 March 2014]

Ebcioğlu, Kemal. “An Expert System for Harmonizing Chorales in the Style of J.S. Bach.” In Understanding Music with AI: Perspectives on Music Cognition. Edited by Mira Balaban, Kemal Ebcioğlu and Otto Laske. Cambridge, MA: AAAI Press & MIT Press, 1992, 295–333.

Forgy, Charles. “Rete: A Fast Algorithm for the Many Pattern / Many Object Pattern Match Problem.” Artificial Intelligence 19/1 (September 1982), pp. 17–37.

Granroth-Wilding, Mark, and Mark Steedman. “Statistical Parsing for Harmonic Analysis of Jazz Chord Sequences.” ICMC 2012: “Non-Cochlear Sound”. Proceedings of the 2012 International Computer Music Conference (Ljubljana, Slovenia: IRZU — Institute for Sonic Arts Research, 9–14 September 2012). http://www.icmc2012.si

Harte, Christopher, Mark B. Sandler, Samer A. Abdallah and Emilia Gómez. “Symbolic Representation of Musical Chords: A Proposed syntax for text annotations.” ISMIR 2005. Proceedings of the 6th ISMIR International Conference on Music Information Retrieval (London, UK: Queen Mary, University of London, 11–15 September 2005). http://ismir2005.ismir.net

JBoss Drools team. “Drools Documentation” [Version 6.0.0.Final]. Available online at http://docs.jboss.org/drools/release/6.0.0.Final/drools-docs/html/index.html [Last accessed 6 March 2014]

Kröger, Pedro, Alexandre Passos, Marcos Sampaio, and Givaldo de Cidra. “Rameau: A System for Automatic Harmonic Analysis.” ICMC 2008. Proceedings of the International Computer Music Conference (Belfast: SARC — Sonic Arts Research Centre, Queen’s University Belfast, 24–29 August 2008).

Laitz, Steve. The Complete Musician: An Integrated approach to tonal theory, analysis and listening. 3rd edition. New York: Oxford University Press, 2012.

Mauch, Matthias. “Automatic Chord Transcription from Audio Using Computational Models of Musical Context.” Unpublished PhD thesis, Queen Mary, University of London, 2010. https://qmro.qmul.ac.uk/jspui/handle/123456789/451

Mauch, Matthias, and Simon Dixon. “Simultaneous Estimation of Chords and Musical Context from Audio.” IEEE Transactions on Audio, Speech and Language Processing 18/6 (August 2010), pp. 1280–1289.

Mauch, Matthias, Katy Noland and Simon Dixon. “Using Musical Structure to Enhance Automatic Chord Transcription.” ISMIR 2009. Proceedings of the 10th ISMIR International Society for Music Information Retrieval Conference (Kobe, Japan: Kobe International Conference Center, 26–30 October 2009). http://ismir2009.ismir.net

Maxwell, John H. “An Expert System for Harmonizing Analysis of Tonal Music.” In Understanding Music with AI: Perspectives on music cognition. Edited by Mira Balaban, Kemal Ebcioğlu and Otto Laske. Cambridge MA: AAAI Press & MIT Press, 1992, pp. 335–353.

Roig-Francolí, Miguel. Harmony in Context. 2nd edition. New York: McGraw-Hill, 2011.

Sapp, Craig Stuart. “Computational Chord-Root Identification in Symbolic Musical Data: Rationale, Methods, and Applications.” Computing in Musicology 15 (2007), pp. 99–119.

Taube, Heinrich. “Automatic Tonal Analysis: Toward the Implementation of a Music Theory Workbench.” Computer Music Journal 23/4 (Winter 1999) “Tonal Analysis and Genetic Techniques,” pp. 18–32.

Temperley, David, and Daniel Sleator. “Modeling Meter and Harmony: A Preference-rule approach.” Computer Music Journal 23/1 (Spring 1999) “Modeling Meter and Harmony,” pp. 10–27.

Wiggins, Geraint, Eduardo Miranda, Alan Smaill and Mitch Harris. “A Framework for the Evaluation of Music Representation Systems.” Computer Music Journal 17/3 (Fall 1993) “Music Representation and Scoring (1),” pp. 31–42.

Winograd, Terry. “Linguistics and the Computer Analysis of Tonal Harmony.” Journal of Music Theory 12/1 (Spring 1968), pp. 2–49.