Partch Harp

Description of Two Special Tunings for the Acoustic Harp and Yamaha DX7-II FD Synthesizer

by Manfred Stahnke

The duo Partch Harp, for acoustic harp and synthesizer (originally a Yamaha DX7‑II FD, but also possible with DX7 emulations or a microtonally tunable computer system plus keyboard, with harp-like sound) was written in 1987/89 for a harp in scordatura, containing “natural” just major thirds (5/4) and “natural” just minor sevenths (7/4). The numbers 5 and 7 can be thought as partials of a fundamental tone “1” of course. There exist several of these “fundamentals” on the harp via its tuning.

The synthesizer’s tuning follows the harp tuning and allows Filtered Just Intonation (for these intervals only!) for any played pitch up and down with a deviation against true 5/4 or 7/4 of less than 1 cent (the tuning is the 12th root of 1.9560685). This means a 12-TET of a narrow “non-octave” 1.9560685/1. The author used a DX7‑II FD, because at that time it was the only freely tunable digital synthesizer. For playing the piece on a DX7‑II FD, the author could deliver a diskette for the synthesizer.

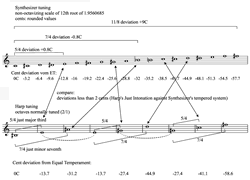
The way of thinking in “integer numbers” looks quite mathematical, but it is very much linked to how our hearing works, at least in certain aspects. Apparently, the auditory system tends to simplify what it receives: If we listen to a so-called tempered interval, the ear adjusts these intervals mentally to the simpler forms, and will accept a “distuned” third as a “natural” third with some added noisy features, like beating or roughness. On the other hand (better: “ear”), our hearing tends toward “scale simplification”: if we hear pentatonic music, based on superimposed 3/2s (fifths), we tend to realise an “even” scale, though the interval steps are sometimes seconds, sometimes minor thirds. In the Western tonal concept, a hypothetical evenness of 12 steps per octave was achieved with Werckmeister and post-Werckmeister tunings, a well known fact, allowing free “transpositions” of diatonic contexts. This new freedom added “noisiness” to thirds and fifths, but it maintained octaves. In my piece Partch Harp however, in spite of the Just Intonation basics, the “noisiness” becomes a well incorporated part and is broadly enlarged. It also includes octaves. If the deviation from a simple (integer ratio) interval is too big, then our hearing cannot adjust anymore and detects a “wrong” interval. The amount of such a deviation varies depending on the type of the integer ratio. For 2/1 (octave) even very small aberrations of 1 or 2 cents can cause the feeling of a “distuned” interval, mainly in the medium register where our hearing has its best resolution. Almost the same is true for 3/2 (fifth). The intervals 5/4 or 6/5 (major and minor thirds) are far less responsive for the feeling of “wrongness” when distuned. But put on top of each other — as is the case quite often in Partch Harp for many supposedly well known intervals — the resulting intervals give an harmonic strangeness very much contrasting to the basic Just Intonation. This is especially true for my octaves and fifths. True 2/1 octaves occur in the harp tuning, but definitely not in the synthesizer tuning. Imagine three 5/4 just thirds put on top of each other: C‑E‑G#‑B#. The added up deviation from the octave C–c (C2–C3) is almost a quarter tone. This is true for my harp as well as my synthesizer. Let us look at the seconds of my synthesizer tuning: The minor seconds are “short” by 3.5 cents (against equal temperament). If you superimpose seven of them to get a fifth, this strange “fifth” is “flat” by 7 x 3.5 = 24.5 cents, a very audible eighth tone. The strange — or charming — feature of Partch Harp is that the harp is tuned in perfect octaves, but the synthesizer is not. By this I get a strangely drifting vessel in an ocean of well tuned asymmetry. Since the synthesizer has no octaving scale, it deviates the more from the harp the higher or lower the register is. As for the title, Harry Partch (1901–74) gave me many ideas about dealing with harmony, or pitches in general. I studied with his companion Ben Johnston for one year in 1979–80 in Urbana-Champaign, Illinois. Partch invented a just-tuned 43‑tone scale, and to play it, he built his own instrumentarium. His music incorporates Just Intonation, but Partch made also use of a manifold harmonic “strangeness” by linear use of his 43 pitches per “octave” 2/1.

The movements of Partch Harp are: Zwiegesang (double chant), Partch Harp, Partch Bourdon and Partch en ciel.

Bibliography

Stahnke, Manfred. Den Ton Finden. Hamburg: Stahnke-Verlag, 2010, pp. 69–102.

_____. “Partch Harp. (Er)Findung einer nicht-oktavierenden Musik.” Musikkulturgeschichte: Festschrift für Constantin Floros zum 60. Geburtstag. Edited by Peter Petersen. Wiesbaden: Breitkopf & Härtel, 1990, pp. 11–26.