Musical Behaviours

Algorithmic composition via plug-ins

by Bruno Degazio

Background

For several decades, the functionality of commercial musical composition software such as Cubase and Logic has been dominated by the simulation of the multi-track tape recorder, in which composition is expressed as the layering of recorded performances, captured via MIDI or audio recording. Support for algorithmic processes in the compositional procedure is virtually non-existent in such software.

Furthermore, in other non-commercial software programmes that do support algorithmic composition, the algorithmic processes are always applied in a “monolithic” manner in which the process has a global scope, taking over the composition completely from beginning to end and through all instruments. While this is sometimes a desirable æsthetic choice to emphasize the unity of the composition, in many cases the algorithmic process interferes with details arising from non-algorithmic aspects of the project. For example, in music composed for the screen it is rare that a single algorithmic process follows the implied narrative or the design of the images throughout.

In recent research I have sought to solve these two different but related problems — on the one hand, the lack of support for algorithmic processes in commercial software; on the other, the lack of controlled scope in non-commercial software. Following an approach developed in Apple’s Motion software, I call these algorithmic processes “behaviours”. The goal of this software design is to make algorithmic processes as transparent to use in compositional practice as any recording or editing operation.

The Context Of “Practical Composition”

“Practical composition” is an important premise in this software design. It is defined here as the hands-on production of any musical work, but especially the following:

• A musical work for accompaniment of a film, video or play;
• Music that follows a narrative structure, such as programme music;
• Music intended for live instrumental performance.

In each of these situations there are numerous “practical” constraints the composer must constantly evaluate. For example, in the first two cases the music must follow the time evolution of an externally imposed, non-algorithmic narrative. In the third case, the practical demands of instrumental performance limit the musical output of an algorithm in numerous ways, from pitch range to breathing or bowing changes.

Although there are many situations where it would be desirable to assist the compositional process algorithmically, this assistance has to be custom shaped to fit the narrative or to accommodate the limitations of acoustic instruments. This means that a form of ad hoc musical control (such as used in the timeline-based automation of a commercial sequencer) must co-exist with the algorithmic process.

The needs of any particular individual narrative moment may require an algorithm ranging in complexity from “raise dynamics logarithmically over eight measures” (i.e. a crescendo), to an astro-physics simulation or chaotic fractal structure. In fact, practical musical composition frequently requires many of these simultaneously. This means that the implementation must allow algorithms to combine correctly when applied simultaneously.

Related Work and Design Influences

Current developments in commercial MIDI sequencers suggest that they may expand their approach to include a limited support of algorithmic composition. In 2014, Apple implemented MIDI FX, a scripting language and a category of software components, into Logic Pro X. Logic’s MIDI FX selection currently offers only simple note processing such as pitch transposition and velocity limiting, along with an arpeggiator and automatic chord trigger. There is some development activity in the Logic Pro X user community to augment these functions with custom scripts. So far the scripts seem to attempt mainly to remedy performance problems such as MIDI continuous control re-direction, and there are few, if any, compositional features beyond the built-in arpeggiator. Some other sequencers such as Cakewalk and Reaper also incorporate scripting languages with varying degrees of flexibility.

Being a full-scale programming environment, Max/MSP is closer to an ideal solution. In principle, most of the plug-in behaviours described here could be programmed in Max/MSP, but to my knowledge no one has attempted anything on this scale.

Another influence on the design of the implementation is the modular analogue synthesizer. Many simpler behaviours correspond closely to function generators in a modular synthesizer. For example, the line behaviour described below is a type of envelope generator and the sine wave behaviour is a type of low frequency oscillator.

Like commercial music sequencers, commercial image animation software such as Autodesk Maya, Adobe After Effects and Apple Motion employ a layered “multi-track” approach. But unlike sequencers, they also provide sophisticated tools for the algorithmic creation and manipulation of moving images. They manage to do so with precision and flexibility, and without limiting non-algorithmic “hand-crafted” details. This type of software is the most immediate precedent for the work described here.

Apple’s Motion has been a particular inspiration for behaviours on the Transformation Engine, because of the originality of its design and the elegance of its implementation. After Effects, Maya and other digital animation software also include many plug-ins that produce dynamic effects, from simple line-based key frame animation to nature-simulating particle systems.

While these software systems are the closest precedents for the author’s own work, none deal with specifically musical requirements.

Desiderata For Algorithmic Composition In The Context Of Practical Composition

To summarize the above considerations, behaviours must:

• Be user selectable (i.e. plug-in format) with a wide choice of algorithms;
• Have clearly defined scope (i.e. limited to a specific time segment and instrument;
• Co-exist with conventional timeline-based automation;
• Combine correctly when applied simultaneously;
• Be interactive in real time, with real-time audio output and graphic display;
• Allow programmable interconnection between one another.

Behaviours

What is a Behaviour?

A behaviour is a user-selectable algorithmic process applied to a single instrument throughout a single section of a composition. The limitations to a single instrument and to a single section mean that the algorithmic process has a clearly defined local scope. These characteristics satisfy the first two items on our list of desiderata. Behaviours exist in a “plug-in” format similar to image-processing plug-ins in After Effects. The current implementation allows up to 12 behaviours to be layered cumulatively on a single instrument or musical segment.

Currently the following plug-in categories are available, each having several choices:

• Shapes. Line Segment with curvature, sine wave, low frequency oscillator, simple attack-release envelope.
• Randomness. Perlin noise, bilinear exponential noise.
• Schillinger. Processes derived from Joseph Schillinger’s system of musical composition.
• Simulations. Processes based on physical simulation such as gravity, wind gust, water drop and double pendulum.
• Fractals and Chaos. Includes Koch Snowflake, logistic equation, multi-species ecological interaction.
• Delay. Simple delay, arpeggiating delay line.
• Utilities. Route one process into to another.
• Timing. Processes in this category affect note onset timing.

Behaviours co-exist with the Transformation Engine’s timeline-based automation, allowing the seamless blending of algorithmic processes with the “hand-crafted” details necessary in the context of practical composition. For example, when applied to a clarinet part, a logistic chaos behaviour may force a pitch interval that is impossible for a player to execute. This can be overcome by applying a change in the timeline automation at the awkward interval only, without changing the algorithmic process elsewhere. This characteristic satisfies desideratum number three.

Behaviours are dynamic, that is, they produce a continually changing output. Each behaviour is directed toward a specific musical target, such as the instrument’s pitch, loudness or note duration.

Behaviours can range in complexity from simple “shapes” (a straight or wavy line) to physics simulations (gravitational acceleration) to chaotic processes, such as the logistic equation and the Lotka-Volterra system for simulating biological species interactions. Multiple behaviours may be applied simultaneously with a cumulative effect, satisfying desideratum number four (that they combine correctly when layered.) The total number of behaviours that can be used in a single composition is unlimited.

Behaviours can operate on one another through a simple data-sharing mechanism. For example, it is quite easy to have a line behaviour control the frequency of a sine wave behaviour (Fig. 2). This characteristic satisfies desideratum number 6: programmable interconnection.

Behaviours Are Real-Time and Interactive

All behaviours work interactively in real time (desideratum number 5). All parameters can be adjusted via a control panel with immediate visual feedback from the Transformation Engine’s composition window and can be operated in real time while listening to the output via a connected MIDI synthesizer. Each behaviour is targeted toward a particular, user-selectable musical parameter, such as tessitura (pitch location) or dynamics (note velocity and expression controller). Every behaviour has a uniquely instantiated set of controls so that parameters can be tailored to the musical context.

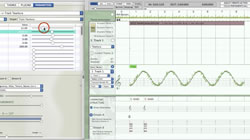
Behaviours Can Be Layered

When more than one behaviour is applied to a given parameter, the outputs are summed to give a combined result. Behaviours can therefore be layered onto one another in a single section of music without interfering with one another. Figure 1 shows a sine wave behaviour combined with a rising line behaviour.

Behaviours can also be made to modify one another’s parameters. Figure 2 shows a line behaviour modifying the wavelength parameter of a sine wave behaviour.

Behaviours Based On Shapes

The simplest behaviours are derived from geometric shapes. These behaviours correspond closely to signal generators, such as the envelope generator (EG) and low frequency oscillator (LFO), in a modular synthesizer.

Line

A line is perhaps the simplest shape possible. It has an inherent dynamism because one end is different from the other. Lines are the building blocks of envelope generators. Applying lines to various musical parameters such as pitch or loudness can produce many common musical gestures and forms. For example, a simple pattern of alternating eighth notes will, with the line behaviour applied to pitch, produce a musical pattern in continuously rising transposition across the span of an octave (Fig. 3).

Note that although pitch is used in most of the examples in this paper, behaviours can be targeted to many other musical parameters. For example, when a line behaviour rising from 32 to 127 is applied to dynamics (in this case note velocity) it will produce a musical crescendo from near-silence to fortissimo (Fig. 4).

Or the line can be applied to note-length, creating a movement from staccato to legato (Fig. 5).

Line behaviours are controlled via the start value, ending value, duration and curve. The curve (or shape of the line) can vary from exponential through linear to logarithmic. The line-shaping algorithm is taken from F. Richard Moore’s Elements of Computer Music (1990). Video 2 demonstrates the interactive use of the line behaviour.

Sine Wave

The Sine wave behaviour applies a sine wave shape to the selected musical parameter. The amplitude, wavelength, phase and damping of the wave are user controllable. It’s surprising how often this simple circular motion suffices to maintain activity in a musical line. The low frequency oscillator behaviour elaborates the sine wave, with the addition of simultaneous outputs for triangle, saw tooth and width-controllable square wave (Fig. 6; Audio 3).

Random Number Behaviours

A basic requirement for many algorithmic processes is a reproducible source of coherent random numbers. For real-time use, the most important characteristic of the generator is that it must be capable of efficiently reproducing a random number at any desired time point. Reproducible means that, for a given input, (typically a seed value and a time location) the generator produces the same output. Coherency means that the numbers vary smoothly with time.

Unfortunately, the random number generator included in most programming languages is not suitable for this purpose, due to its lack of efficiency. In theory, any software random number generator is capable of reproducing a series of (quasi-) random numbers from a given seed value. The problem arises when a particular item in the random number series is required. For example, the 10,000th item in the series might be immediately needed, but a typical programming language random number generator would have to compute the previous 9,999 items before being able to produce item 10,000. Naturally this makes such a generator unusable for interactive purposes.

This problem was recognized some years ago in the field of animated computer graphics, where Ken Perlin, then working for the Walt Disney Company, devised a solution for which he received an Academy Award for Technical Achievement in 1997. This solution, now called Perlin Noise, is commonplace in computer animation software. Transformation Engine behaviours use a form of one-dimensional Perlin Noise for all random processes.

Perlin Randomness Behaviour

The Perlin Random behaviour is the fundamental random number generator used in the Transformation Engine. It can be applied to any Transformation Engine parameter, such as pitch, velocity, dynamic continuous controller, note length, etc. Perlin noise is controllable via the number of octaves of noise used and a “jitter” control which determines the balance between high and low frequency noise — high frequencies produce a more jittery output. The noise seed is user-settable, allowing different but reproducible series of random numbers for various applications (Figs. 7–8).

Randomly Drop Notes, Randomly Multiply Notes into Chords

The same Perlin random generator can be used to completely eliminate notes on a random basis. The seed, number of octaves and jitter controls are the same as in the basic random generator.

Similarly, individual notes can be randomly turned into chords, the pitches being determined by the currently active global harmonic parameters such as key, scale mode and chord voicing preferences.

Time-Distortion Behaviour

Line Segment Timing

The line behaviour can be targeted to timing related parameters, producing a continuous distortion of musical time. Figure 11 shows a line behaviour approximating a simple attack-sustain-release envelope, applied to a flute motif so that the flute line accelerates towards the centre of the phrase and decelerates at the end. Meanwhile, the accompanying piano, which has no time-distorting behaviour installed, plays in steady quarter notes (Audio 4).

Behaviours Based On Fractals and Chaos

The study of chaotic processes and fractals has provided many interesting algorithms useful in musical composition. The Transformation Engine includes behaviours based on the Koch curve (sometimes known as the “snowflake” fractal), the logistic equation, multi-species ecological modeling and others.

Koch Snowflake

The Koch “Snowflake” fractal is one of the simplest fractals to understand graphically, and its application to musical structure is similarly obvious. The fractal is generated by the recursive application of a simple graphic shape called the “generator”. In the classic visual form, the generator is an equilateral triangle. In a musical application the generator would more aptly be called a “motif”. The generator is the musical interval of a rising fifth applied recursively seven times, producing a pattern of 128 notes related self-similarly.

Logistic Equation

The logistic equation is one of the earliest chaotic models, originating in 19th-century biological studies of the predator-prey relationship, such as encountered in fox and rabbit populations. Though simple to implement, it produces a wide and musically useful variety of chaotic patterns. The biological origins of the logistic equation have been further developed in 20th-century studies of multi-species predator-prey webs. Figure 12 shows the control panel for the multi-species behaviour. Figure 13 shows the outputs of the model’s four species targeted to note pitch for a quartet of woodwind instruments.

Physics-Based Behaviours

The representation of nature is (arguably) the purpose of art. To that end several behaviours were implemented, including:

• Gravity — a simulation of projectile flight;
• Water waves — a simulation of wave motion produced by wind on the surface of the sea;
• A wind gust simulator;
• A particle system emitter.

Gravity

The gravity behaviour simulates the physics of projectile motion, including both initial flight and bouncing at impact with the ground plane. Several controls are available to fine-tune the physical simulation, including acceleration (i.e. gravitational force), initial velocity of the projectile, ground level and bounce efficiency.

Ocean Waves

The movement of water in its many forms has long been a source of fascination to artists and composers. The sine wave behaviour provides a highly simplified form of wave motion, but a more complex version has been developed in the field of oceanography by means of analysis of the spectral content of ocean waves, breaking the motion into the sum of many irrationally related (i.e. non-harmonic) sine waves. The principal control parameter in the simulation is wind speed, measured in knots (nautical miles per hour). Figure 15 shows the non-linear effect of a wind speed of 26 knots.

Particle System Emitter

A simple particle system can be built by using several instances of the particle emitter behaviour. Each musical “particle” requires its own track, so the system is limited to a relatively small number of particles; unlike in a visual particle system, where they may number in the thousands or millions.

Musical Examples

Wind Gust Scene from “Land of the Silver Birch”

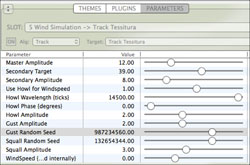
This section illustrates the use of behaviours in a typical compositional context — the orchestral representation of nature in Land of the Silver Birch, a composition consisting of traditional music from Ontario, Canada’s largest province. A portion of the composition uses the wind gust behaviour to depict wind blowing through marshland reeds near Georgian Bay, the traditional home of the Huron Indians.

The wind gust behaviour is derived from an algorithm given in Andy Farnell’s 2010 book, Designing Sound. The primary controls for the wind gust algorithm are amplitude levels called howl, gust and squall. These control the amount of noise components with approximate centre frequencies of 0.1 Hz, 1 Hz and 10 Hz, respectively.

A piano is used to depict the wind gust. A simple motif consisting of four sixteenth notes is the raw material. Without a behaviour applied, the motif simply repeats in the manner of an ostinato, except for transpositions to fit global harmonic changes.

Next, applying the wind gust behaviour gives an interesting new pitch contour. The erratic quality is a result of the three levels of randomness generated by the algorithm. Note that the dynamic contour is similar to the pitch contour but is not shown in Figure 18.

Lastly, to eliminate the steady sixteenth pattern, a timing pattern behaviour is applied to note inter-onset durations, giving a variety of rhythmic pace by using triplets and quintuplets as well as sixteenth notes (Audio 11).

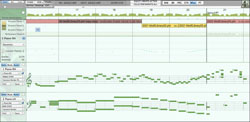
“Rubato Roboto”

A short composition for piano using musical behaviours has been created. The piece Rubato Robato is a computerized parody of the stride piano style of the 1930s, with a particular nod to Art Tatum. The title refers to the prominent use of time-based behaviours that produce a sense of fluidly changing rhythm, as in musical rubato (Fig. 20; Audio 12). Other behaviours used in this piece include the sine wave and fade in / fade out behaviours applied to pitch and dynamics.

Conclusion

A variety of algorithmic processes have been implemented as user-selectable plug-ins. The plug-in format allows for novel styles of algorithmic composition by facilitating the combination of algorithmic processes to produce a desired musical result. This is in contrast to commercial composition software (sequencers), which do not support algorithmic composition in a substantial way, and to experimental composition software such as Max/MSP or Pd, which support algorithmic processes only in a global manner.

These “musical behaviours” provide a software composition environment suitable for “practical composition” by fulfilling the desiderata listed at the beginning of this article. Specifically, a behaviour in the Transformation Engine:

• Is user selectable (i.e. a plug-in format) with a wide choice of algorithms.
• Has a clearly defined scope (i.e. is limited to a specific time segment and instrument.)
• Combines correctly with other behaviours operating simultaneously (i.e. is layerable.)
• Co-exists with timeline-based automation.
• Is interactive in real time, with audio output and graphic display.
• Allows programmable interconnection with other behaviours.

Bibliography

Bernard, Jonathan W. “The Evolution of Elliott Carter’s Rhythmic Practice.” Perspectives of New Music 26/2 (Summer 1988), pp. 164–203.

Degazio, Bruno. “The Schillinger System and Contemporary Computer Music.” Presented at the Diffusion conference (Toronto: Canadian Electroacoustic Community, 1989).

_____. “The Transformation Engine.” ICMC 2004. Proceedings of the 30th International Computer Music Conference (Miami FL, USA: University of Miami, 1–6 November 2004).

_____. “Integrating OpenGL Into the Transformation Engine. Presented at the 2011 Toronto Electroacoustic Symposium.

Farnell, Andy. Designing Sound. Cambridge MA: The MIT Press, 2010.

Moore, F. Richard. Elements of Computer Music. Upper Saddle River NJ: Prentice-Hall, 1990.

Perlin, Ken. “Improving Noise.” Computer Graphics 35/3. ACM Siggraph, 2001.

Standard for Perlin Noise — US Patent 6867776 B2 — S(2002).